Remarque
La notion de « charge à courant complexe constant » est ambiguë : selon les auteurs et les situations, ce terme peut désigner soit une charge dont le module du courant et son déphasage par rapport à la tension sont imposés, soit une charge dont le module du courant et sa phase (absolue) sont imposés. Nous traitons ici le deuxième cas de figure. Le premier correspond à une charge non-linéaire, comme les charges à puissance constante ; cf la partie 4.11.
La charge à courant complexe constant n’est guère physique, dans la mesure où elle impose non seulement l’amplitude mais aussi la phase du courant concerné ; or, le choix de l’origine des temps étant arbitraire, les phases le sont également : l’origine des phases est fixée en un certain nœud, généralement en un nœud dit « racine » (ou « slack » en anglais) où l’on fixe à zéro l’argument du phaseur de tension sur la phase A, et elle ne doit ensuite être imposée en aucun autre nœud. Pour le dire autrement : le fait de retarder les tensions du nœud-racine d’un certain angle $\theta$ est une modification sans importance physique (on change simplement l’origine arbitraire du temps) qui doit simplement retarder tous les phaseurs de tension et de courant dans le réseau de ce même angle $\theta$, et donc ne pas affecter les valeurs des grandeurs mesurables comme les modules des courants et des tensions ou les flux de puissance active et réactive. Or, les charges à courant complexe constant ne vérifient pas cette propriété, ce qui les rend hautement suspectes : un tel modèle ne devrait donc a priori jamais apparaître dans un modèle de réseau, sauf peut-être dans des cas très particuliers.
En revanche, les charges à courant complexe constant peuvent apparaître comme intermédiaire de calcul dans certaines méthodes de résolution itératives ; la partie 7, qui illustre l’utilisation de la théorie des composantes symétriques pour résoudre un problème de load flow triphasé à partir d’un solveur de load flow monophasé, présente un exemple de cette situation. Dans ce cas, le modèle de charge à courant complexe constant ne figure pas dans le modèle de réseau initial, mais il est utilisé de façon passagère et invisible à l’utilisateur, à l’intérieur du solveur, en tant qu’artifice mathématique de résolution des équations de load flow. C’est ce cas de figure qui motive l’introduction de ce modèle, et qui le rend utile malgré sa faible pertinence physique.
Mise en équations en coordonnées usuelles
Soit $\iota \in \C^3$ la valeur des trois courants de phase que l’on cherche à imposer.
Les équations en coordonnées usuelles sont :
\begin{equation}
\begin{cases}
I_{ABC} = \iota \\
\un^\top \, I_{ABC} + I_N = 0.
\end{cases}
\end{equation}
Le composant dispose de 8 variables, qui sont toutes des variables de port, et de quatre équations ; donc de 4 degrés de liberté, comme on s’y attend pour un composant à quatre ports.
Les sous-matrices $3 \times 3$ qui interviennent dans ce système sont la matrice nulle et la matrice identité $I_3$ : elles sont toutes deux invariantes par changement de base. On s’attend à ce que, dans les trois systèmes symétriques, les coefficients des variables symétriques soient identiques.
Remarque
Le passage en composantes symétriques n’a donc aucun intérêt en terme de simplification des équations de la source, hormis l’avantage mineur de rendre un peu plus concis le paramétrage d’une source équilibrée, par une seule valeur (sa tension directe) au lieu de trois. Simplement, si l’on se place dans le cas où l’on a décidé de modéliser l’ensemble du réseau en composantes symétriques parce que cela est avantageux pour d’autres composants, alors il faut aussi effectuer le changement de variables sur les charges à courant complexe constant. Nous avions déjà fait une observation analogue à propos des composants asymétriques, comme la plupart des défauts, à la Remarque 25 : dans le cas des défauts, le passage en composantes symétriques n’a pas d’intérêt parce qu’il ne simplifie pas les équations, et dans le cas des charges à courant constant, il n’a pas d’intérêt parce que les équations sont déjà triviales en coordonnées usuelles (et le restent, ni plus ni moins, en coordonnées symétriques).
Changement de base
On effectue le changement de base sur les variables et sur les équations :
\begin{equation}
\begin{cases}
I_{0id} = F^{-1} \, \iota \\
3 I_0+ I_N = 0
\end{cases}
\end{equation}
soit
\begin{equation}
\label{eq:modele-sym-charge-I-const}
\begin{cases}
I_d = \iota_d \\
I_i = \iota_i \\
I_0 = \iota_0 \\
I_0 + \tilde{I}_N = 0.
\end{cases}
\end{equation}
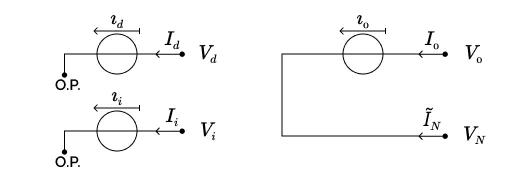
Comme attendu, les coefficients des variables $I_0$, $I_i$ et $I_d$, après diagonalisation de l’unique bloc triphasé d’équations, sont égaux entre eux (et égaux à $1$).
L’équation directe est équivalente à une charge (monophasée) à courant constant de valeur $\iota_d$ placée entre le port $(V_d, I_d)$ et l’origine des potentiels~; l’équation inverse est de même équivalente à une charge à courant constant de valeur $\iota_i$ placée entre le port $(V_i, I_i)$ et l’origine des potentiels~; et l’équation homopolaire est équivalente à une charge à courant constant de valeur $\iota_0$ placée entre le port $(V_0, I_0)$ et le port $(V_N, \tilde{I}_N)$.
Remarque
Comme nous l’avons signalé en introduction de ce chapitre, le modèle 4.16 de la charge à courant constant est toujours découplé, quelle que soit la valeur du courant imposé $\iota$. En ce sens, la charge à courant constant est toujours symétrique, même lorsque les courants que l’on impose ne forment pas un système triphasé équilibré.
Pour les autres modèles de charge usuels, on parle généralement de charge « équilibrée » ou « déséquilibrée », ou de façon équivalente de charge « symétrique » ou « asymétrique », selon que l’hypothèse de symétrie est respectée ou non. Pour les charges à courant constant, cette distinction n’existe pas~: il n’y a pas de raison de parler de charge à courant complexe constant en la qualifiant spécifiquement de « symétrique » (elle l’est toujours) ou « asymétrique » (elle ne l’est jamais). En revanche, on parle parfois de charge à courant constant « équilibrée directe » (respectivement équilibré indirecte, respectivement purement homopolaire) pour signifier que le courant imposé sur chaque phase est égal au courant sur la phase précédente multiplié par $a^2$ (respectivement par $a$, respectivement par $1$). De même, on parle parfois de charge à courant complexe constant « déséquilibrée » lorsque la charge à courant constant n’est ni équilibrée directe, ni équilibrée indirecte, ni purement homopolaire, au sens précédent. Il ne faut cependant pas perdre de vue qu’une telle « charge déséquilibrée » est bien symétrique au sens de la théorie des composantes symétriques.
Schéma électrique symétrique
Les schémas équivalents sont présenté ci-dessous :
Variante à neutre non-accessible
Si le neutre n’est pas accessible, alors on passe à un composant à 3 ports caractérisé a priori par 7 variables (6 variables de ports et le potentiel du point neutre). Le potentiel du point neutre est néanmoins indéterminé et ne mérite pas vraiment de figurer dans les équations ; on peut donc plutôt considérer qu’il s’agit d’un composant à 6 variables et à trois équations :
\begin{equation}
\begin{cases}
I_d = \iota_d \\
I_i = \iota_i \\
I_0 = 0, \\
\end{cases}
\end{equation}
soumis à la condition de compatibilité~: $\iota_0 = 0$.