Remarque :
Le « générateur homopolaire » est un dispositif électrotechnique standard qui ressemble beaucoup à celui qui est décrit dans cette section ; la seule différence semble être la présence d’une résistance additionnelle dans le bobinage en triangle. Ce dispositif est utilisé lorsque le plan de protection exige la mise à la terre du neutre en un certain point du réseau, et que l’on n’y dispose pas déjà naturellement d’un point neutre. Dans cette situation, le générateur homopolaire permet de créer le point neutre manquant.
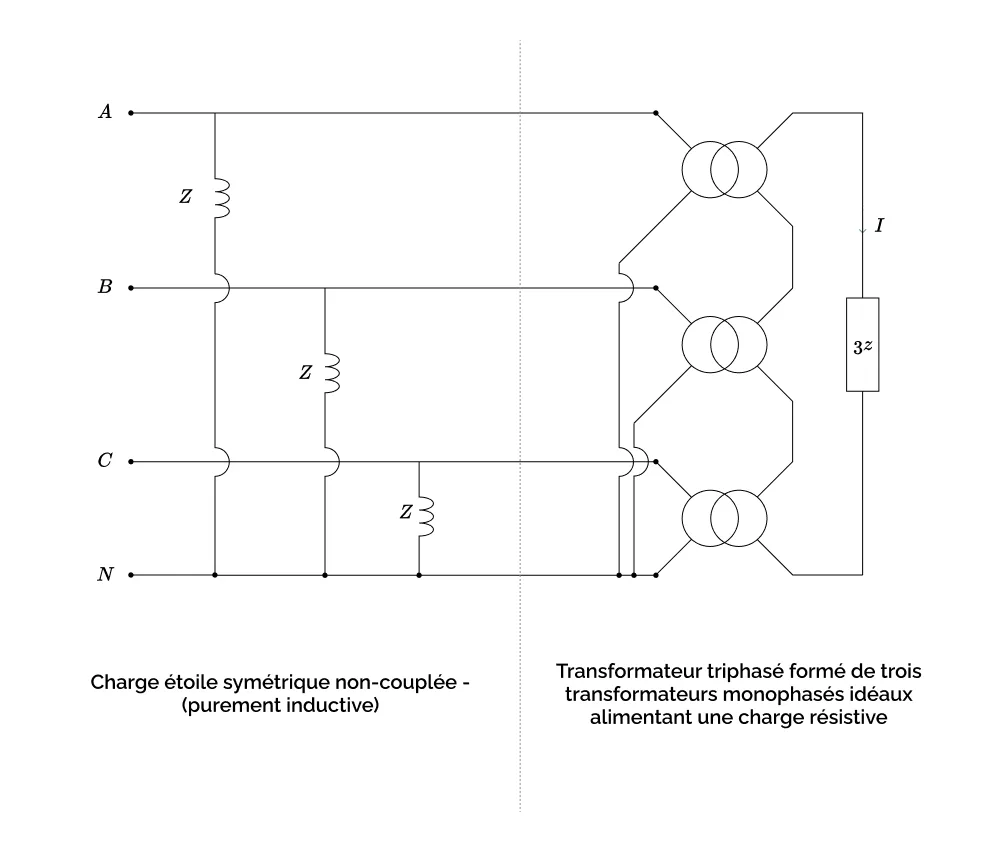
On considère un transformateur étoile-triangle dont le primaire en étoile est couplé au réseau et dont le secondaire en triangle est laissé à vide, ce qui constitue une charge couplée à 4 ports.
On suppose que le transformateur triphasé est constitué par assemblage de trois transformateurs monophasés indépendants. Nous modéliserons ces transformateurs en utilisant le modèle usuel à une seule impédance série, placée au secondaire, que nous avons introduit dans le chapitre 2.
Remarque :
Au prix d’une petite complexification des calculs qui vont suivre, on pourrait aussi utiliser le modèle de transformateur monophasé à deux impédances séries.
Les trois transformateurs sont supposés identiques, ce qui rend l’objet structurellement invariant par permutation circulaire des phases. Leur rapport de transformation, qui n’a pas grande importance dans le cas présent, est supposé égal à 1.
Changement de base sur les triplets de variables triphasées
Effectuons le changement de variables habituel pour passer les deux triplets triphasés en coordonnées symétriques : \begin{equation} \begin{cases} F \, I_{0id} = I \, \un \\ \un^\top \, F \, V_{0id} – 3 V_N = 3 z I \\ \un^\top \, F \, I_{0id} + I_N = 0. \end{cases} \end{equation} soit au vu de 1.9 : \begin{equation} \label{eq:etoile-triangle-rien-post-Fortescue} \begin{cases} F \, I_{0id} = I \, \un \\ V_0 – V_N = z I \\ 3 \, I_0 + I_N = 0. \end{cases} \end{equation}Changement de base sur les blocs triphasés d’équations
Prémultiplions maintenant notre unique bloc triphasé d’équations par $F^{-1}$ pour obtenir, tous calculs faits : \begin{equation} \begin{cases} I_0 = I \\ I_i = 0 \\ I_d = 0 \\ V_0 – V_N = z I \\ 3 I_0 + I_N = 0. \end{cases} \end{equation} Comme attendu, les coefficients des variables symétriques sont égaux (à $1$, pour les trois variables symétriques de courant, et à $0$, pour les trois variables symétriques de potentiels) et en particulier, les systèmes direct et inverse sont bien identiques. On élimine enfin la variable $I$ pour obtenir $$ V_0 – V_N = z I_0, \quad I_0 + \tilde{I}_N = 0, \quad I_d = 0 \quad \mbox{et} \quad I_i = 0. $$Schéma électrique symétrique
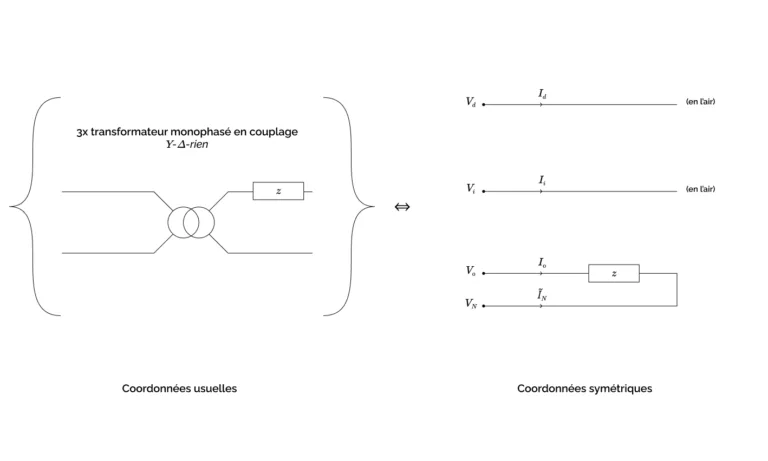
On peut interpréter notre charge de la manière suivante.- dans le circuit direct, elle est équivalente à laisser en l’air le port \((V_d, I_d)\) : en effet, \(I_d\) est nul et \(V_d\) (qui n’apparaît pas dans les équations) est quelconque.
- De même, dans le circuit inverse, elle est équivalente à laisser en l’air le port \((V_i, I_i)\) : en effet, \(I_i\) est nul et \(V_i\) (qui n’apparaît pas dans les équations) est quelconque.
- Enfin, dans le circuit homopolaire, elle revient à placer une impédance \(z\) entre le port \((V_0, I_0)\) et le port \((V_N, \tilde{I}_N)\).
Remarque : L’impédance série $z$ étant normalement très faible, on peut considérer cette charge comme un quasi-court-circuit homopolaire-neutre, associé à une impédance au contraire infinie (avant réintégration des impédances magnétisantes) en mode direct et en mode inverse. Ce composant sera donc transparent du point de vue direct et inverse, tandis qu’il appellera un courant homopolaire potentiellement énorme qui forcera la tension homopolaire-neutre $V_0 – V_N$ à être quasi-nulle (voire nulle si on modélise le composant comme idéal en mettant $z$ à zéro) ; ceci sous réserve, bien sûr, que la source amont soit modélisée comme non-idéale, de sorte que sa tension finira bien par s’effondrer si l’on tire suffisamment de courant. Inversement, si on modélise la source comme idéale et qu’on conserve un $z$ non-nul dans la charge, alors la tension homopolaire-neutre restera inchangée et on aura simplement un courant gigantesque dans la charge ; et enfin, si on modélise les deux composants comme idéaux, alors le problème n’aura pas de solution.
C’est de cet effet de court-circuit homopolaire-neutre que vient l’appellation « d’équilibreur » que l’on donne à ce dispositif : il garantit la (quasi-)disparition d’une certaine forme de déséquilibre en tension, à savoir la présence d’une tension homopolaire-neutre, tout en restant (quasi-)transparent sur la tension directe. On observe cependant qu’il est dépourvu d’effet sur l’autre forme de déséquilibre en tension~: la présence d’une tension inverse.
Réintégration des inductances magnétisantes
Si, pour finir, on réintègre les équations de notre charge étoile purement inductive connectée en parallèle, en sommant les courants symétriques de nos deux objets, et après élimination de la variable interne \(I\), on aboutit pour notre équilibreur étoile-triangle-rien aux équations suivantes :
\begin{equation}
\begin{cases}
V_d = Z I_d \\
V_i = Z I_i \\
I_0 = (\frac{1}{z} + \frac{1}{Z}) (V_0 – V_N) \\
I_0 + \tilde{I}_N = 0.
\end{cases}
\end{equation}
La charge couplée étoile-triangle avec secondaire à vide est donc caractérisée simplement par les trois impédances symétriques suivantes :
$$ Z_d := Z, \quad Z_i := Z \quad \mbox{et} \quad Z_0 := \frac{z \cdot Z}{z + Z} \approx z, $$
(où l’on rappelle que $Z$ est l’impédance parallèle, dite magnétisante, de chacun des trois transformateurs monophasés identiques de rapport $1$ qui constituent le dispositif, et $z$ est leur impédance série). Ces impédances, comme dans les cas précédemment étudiés, s’entendent de la manière suivante : entre le port $(V_d, I_d)$ et l’origine des potentiels pour l’impédance directe, entre le port $(V_i, I_i)$ et l’origine des potentiels pour l’impédance inverse, et entre le port $(V_0, I_0)$ et le port $(V_N, \tilde{I}_N)$ pour l’impédance homopolaire.
Le schéma électrique correspondant est présenté sur la figure ci-dessous :
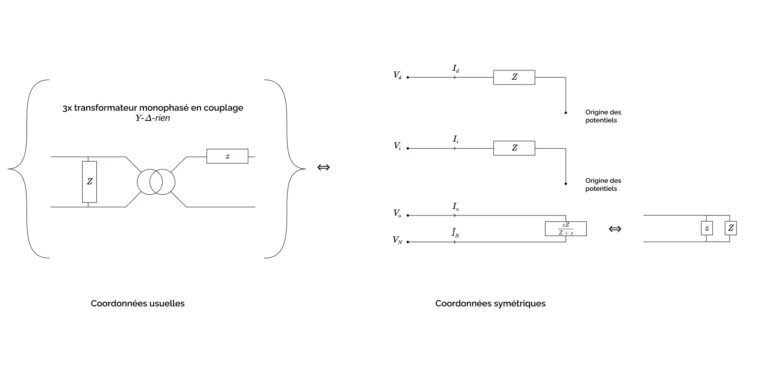
Nous avons démontré dans le chapitre 3 qu’un composant triphasé équilibré passif pouvait être représenté sous forme de trois système découplés direct, inverse et homopolaire, ne faisant respectivement intervenir que les variables directes, inverses, et homopolaires/isolées. Dans le cas d’une charge, qui ne possède qu’un seul triplet triphasé de ports par opposition à une ligne ou un transformateur, on aboutira donc dans le cas du système direct à un système linéaire ne faisant intervenir que $V_d$ et $I_d$, qui se ramènera nécessairement à un seul paramètre numérique que l’on pourra interpréter comme une impédance placée entre le port $(V_d, I_d)$ et l’origine des potentiels, ou éventuellement comme un circuit ouvert (on parlera alors plus d’admittance que d’impédance, et on déclarera cette admittance égale à zéro). Le même raisonnement s’applique au système inverse.
De même, dans le cas du système homopolaire après application du changement de variable $I_n \longrightarrow \tilde{I}_N$, tous les exemples qui sont traités dans ce document se ramènent à une impédance placée entre les ports $(V_0, I_0)$ et $(V_N, \tilde{I}_N)$.
Autrement dit, la théorie des composantes symétriques offre une manière standardisée de décrire une charge triphasée équilibrée, sous la forme de trois « impédances symétriques ».
Ceci permet notamment de comparer facilement deux charges équilibrées qui sont structurellement différentes, comme nous l’avons fait à la Remarque 32 pour la charge étoile à neutre non-relié et la charge triangle, en les ramenant à une description unifiée.
