Intéressons-nous maintenant à l’équilibreur zigzag qui est représenté ci-dessous :
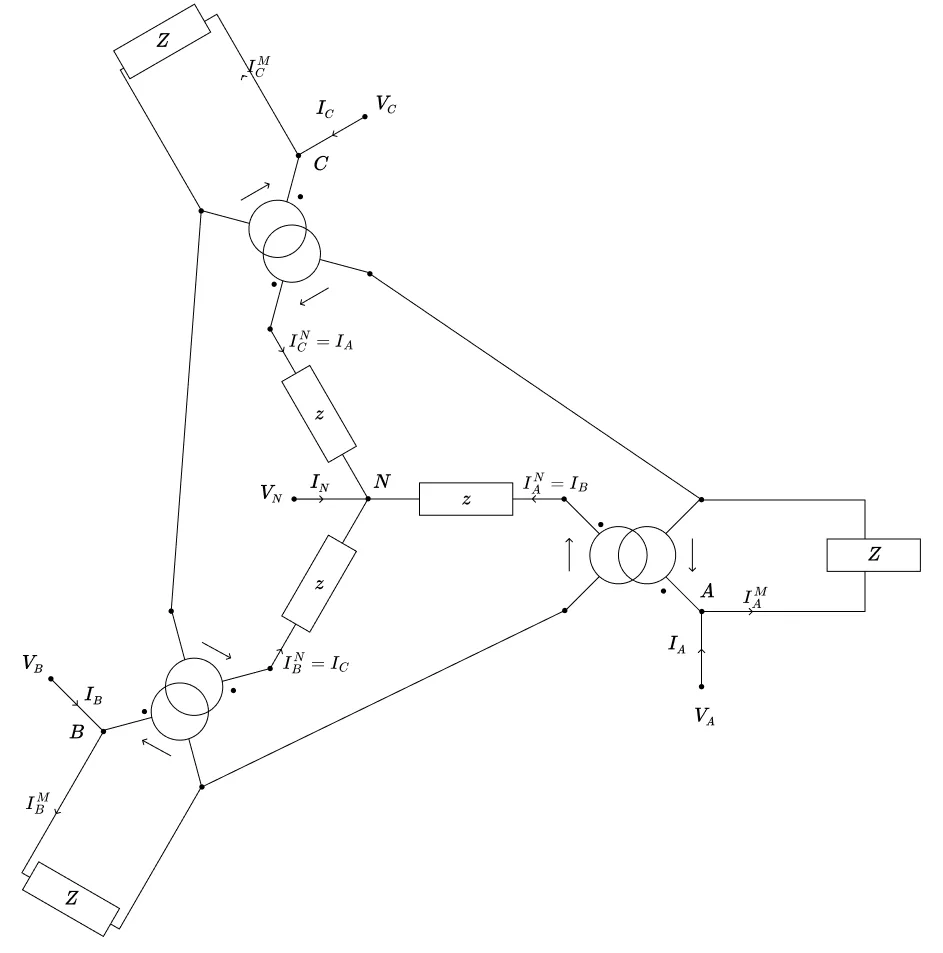
Nous le supposerons constitué de trois transformateurs monophasés de rapport $1$, ce qui nous permettra d’utiliser un modèle classique de transformateur monophasé non-idéal présenté dans le Chapitre 2 ; et identiques, ce qui rendra l’objet invariant par permutation circulaire des ports et nous permettra donc d’appliquer la théorie des composantes symétriques.
Mise en équations en coordonnées usuelles
Les équations en coordonnées usuelles sont les suivantes~:
\begin{equation}
\begin{cases}
I_A^M = I_A – I_B\\
I_B^M = I_B – I_C\\
I_C^M = I_C – I_A\\
V_N + z I_B + Z (I_B^M – I_A^M) = V_B\\
V_N + z I_C + Z (I_C^M – I_B^M) = V_C\\
V_N + z I_A + Z (I_A^M – I_C^M) = V_A\\
I_A + I_B + I_C + I_N = 0
\end{cases}
\end{equation}
soit, par blocs et en faisant apparaître la matrice $S$ que nous avons définie à l’équation 1.3,
\begin{equation}
\begin{cases}
I_{ABC}^M = (I_3 – S) \, I_{ABC} \\
V_N \, \un + z S I_{ABC} + Z \, (S – I_3) \, I_{ABC}^M = S \, V_{ABC} \\
\un^\top I_{ABC} + I_N = 0.
\end{cases}
\end{equation}
Ce composant possède 11 variables~: 8 variables associées à ses 4 ports, et les trois courants magnétisants $I_A^M$, $I_B^M$ et $I_C^M$ qui constituent trois variables internes. Parmi ces 11 variables, on compte 3 triplets triphasés $V_{ABC}$, $I_{ABC}$ et $I^M_{ABC}$, et deux variables isolées $V_N$ et $I_N$.
Le problème compte par ailleurs 2 blocs triphasés d’équations et une équation isolée, soit 7 équations indépendantes au total et donc 4 degrés de liberté comme on s’y attend pour un composant à 4 ports.
Dans le premier bloc triphasé d’équations, la sous-matrice associée au triplet $V_{ABC}$ est nulle, celle associée $I^M_{ABC}$ est égale à $I_3$, tandis que celle associée à $I_{ABC}$ est égale à $S-I_3$. Dans le deuxième bloc triphasé d’équations, les sous-matrices associées aux triplets $V_{ABC}$, $I_{ABC}$ et $I^M_{ABC}$ sont respectivement égales à $-S$, $zS$ et $Z (S-I_3)$. Toutes ces sous-matrices sont circulantes. De plus, dans le premier bloc triphasé d’équations, aucune variable isolée n’intervient, tandis que dans le second, seule $V_N$ intervient et la colonne associée est égale à $\un$. Enfin, dans l’unique équation isolée, le seul triplet de variables triphasées qui intervient est $I_{ABC}$ et la ligne associée est égale à $\un^\top$. La matrice possède donc la structure circulante.
Dans le premier bloc triphasé d’équations, toutes les matrices sont réelles ; au vu de la Remarque 3, on s’attend à ce que les équations directe et inverse qui apparaîtront après la diagonalisation soient conjuguées l’une de l’autre.
Dans le second bloc triphasé d’équations, la première sous-matrice $3 \times 3$ est réelle et les deux autres sont des multiples d’une matrice réelle, avec un facteur $z$ et $Z$ respectivement. A ce facteur près, on s’attend donc à ce que les équations directe et inverse qui apparaîtront après la diagonalisation soient également conjuguées l’une de l’autre.
On observe ici, pour la première fois dans ce document, une situation où l’on n’a pas l’égalité $\beta = \gamma$ de la Remarque 4 : intuitivement, le couplage entre les phases A et B n’est pas le même que le couplage entre A et C, par exemple. Dans cette situation, à première vue, rien ne semble donc garantir que les systèmes direct et inverse seront identiques, alors que c’est ce à quoi l’on s’attend pour un circuit immobile… Nous reviendrons sur ce point à la Remarque 40.
Changement de base sur les triplets de variables triphasées
Effectuons le changement de base sur les trois triplets triphasés qui interviennent dans notre problème :
\begin{equation}
\label{eq:equilibreur-zigzag-post-Fortescue}
\begin{cases}
F \, I_{0id}^M = (I_3 – S) \, F \, I_{0id} \\
V_N \, \un + z S F \, I_{0id} + Z \, (S – I_3) \, F \, I_{0id}^M = S \, F \, V_{0id} \\
\un^\top F \, I_{0id} + I_N = 0.
\end{cases}
\end{equation}
Changement de base sur les blocs triphasés d’équations
Prémultiplions les deux blocs triphasés d’équations par $F^{-1}$ :
\begin{equation}
\begin{cases}
I_{0id}^M = F^{-1} \, (I_3 – S) \, F \, I_{0id} \\
V_N \, F^{-1} \, \un + z F^{-1} \, S \, F \, I_{0id} + Z \, F^{-1} \, (S – I_3) \, F \, I_{0id}^M = F^{-1} \, S \, F \, V_{0id} \\
\un^\top F \, I_{0id} + I_N = 0.
\end{cases}
\end{equation}
Tous calculs faits en exploitant l’équation 1.11, ce système devient
\begin{equation}
\begin{cases}
I_0^M = 0 \\
I_i^M = (1-a) I_i \\
I_d^M = (1-a^2) I_d \\
V_N + z I_0 = V_0 \\
z a I_i – Z (1-a) I_i^M = a V_i \\
z a^2 I_d – Z (1-a^2) I_d^M = a^2 V_d \\
3 I_0 + I_N = 0.
\end{cases}
\end{equation}
Comme attendu, la deuxième et la troisième équation sont bien conjuguées~; et la cinquième et la sixième équation présentent des coefficients de la forme « $z$ fois des nombres complexes conjugués ($a$ et $a^2$) » pour les courants symétriques $I_i$ et $I_d$, et « $Z$ fois des nombres complexes conjugués ($1-a$ et $1-a^2$) » pour les courants symétriques $I_i^M$ et $I_d^M$.
On décompose notre jeu d’équations en trois groupes ; un groupe direct :
\begin{equation}
\begin{cases}
I_d^M = (1-a^2) I_d \\
z I_d + (1-a) Z I_d^M = V_d
\end{cases}
\iff
(z + 3 Z) \, I_d = V_d,
\end{equation}
un groupe inverse :
\begin{equation}
\begin{cases}
I_i^M = (1-a) I_i \\
z I_i + Z (1-a^2) I_i^M = V_i
\end{cases}
\iff
(z + 3 Z) \, I_i = V_i
\end{equation}
et un groupe homopolaire :
\begin{equation}
\begin{cases}
V_0 – V_N = z I_0 \\
3 I_0 + I_N = 0.
\end{cases}
\end{equation}
Remarque 40 :
Tous calculs faits, le système inverse et le système direct sont bien identiques, ce qui n’était pas évident en observant les matrices $3 \times 3$ impliquées dans notre matrice à structure circulante !
Les termes suffixés par $M$, quant à eux, peuvent être complètement éliminés du problème ; si on souhaite les retrouver pour pouvoir remonter aux courants magnétisants, il faut utiliser les formules
$$ I_0^M = 0, \quad I_i^M = (1-a) I_i \quad \mbox{et} \quad I_d^M = (1-a^2) I_d, $$
puis appliquer la transformée de Fortescue inverse.
Schéma électrique symétrique
On peut interpréter le système direct comme une impédance de valeur $Z_d := z + 3 Z$ placée entre le port $(V_d, I_d)$ et l’origine des potentiels~; le système inverse comme une impédance identique ($Z_i := Z_d$), placée entre le port $(V_i, I_i)$ et l’origine des potentiels~; et le système homopolaire comme une impédance $Z_0 := z$ placée le port $(V_0, I_0)$ et le port $(V_N, \tilde{I}_N)$. Le schéma symétrique correspondant est représenté ci-dessous :
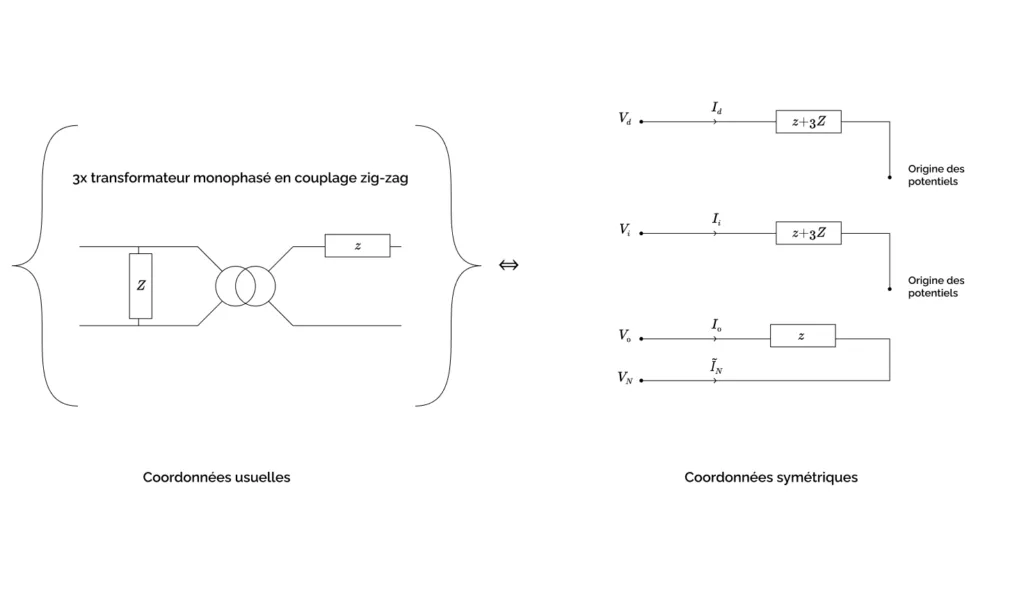
On retrouve l’effet de (quasi-)court-circuit homopolaire-neutre qui caractérise les dispositifs équilibreurs.
Remarque 41 :
L’impédance série $z$ étant normalement très petite devant l’impédance magnétisante $Z$, on a
$$ Z_d = Z_i \approx 3 Z. $$
Remarque 42 :
A la Remarque 39, en généralisant à partir de l’exemple des charges étoile et triangle équilibrées, nous avions observé que toute charge triphasée équilibrée était nécessairement caractérisée par la donnée de trois admittances ou impédances (éventuellement nulles) dites directe, inverse et homopolaire ; respectivement placées entre le port $(V_d, I_d)$ et l’origine des potentiels, entre le port $(V_i, I_i)$ et l’origine des potentiels, et entre les ports $(V_0, I_0)$ et $(V_N, \tilde{I}_N)$. Deux nouveaux exemples, celui du transformateur étoile-triangle avec secondaire à vide et celui l’équilibreur zigzag, viennent d’illustrer de nouveau cette propriété.
Remarque 43 :
Nous avions également observé à la remarque 39 que la donnée de ces trois impédances symétriques était une manière compacte et standardisée de caractériser une charge triphasée équilibrée, ce qui facilite (entre autres choses) la comparaison entre elles de charges structurellement différentes. Nous venons d’observer une nouvelle illustration de cette observation : la caractérisation par des impédances symétriques montre que le transformateur étoile-triangle avec secondaire à vide et l’équilibreur zigzag, qui sont structurellement, très différents, sont en fait fonctionnellement très semblables : ils opposent tous deux une forte impédance en mode direct et en mode inverse, et une impédance très faible en mode homopolaire. De façon plus quantitative, la caractérisation symétrique montre immédiatement qu’une charge couplée étoile-triangle avec les paramètres $(Z, z)$ est équivalent à un équilibreur zigzag avec les paramètres $Z’ := \frac{Z^2}{3(z+Z)}$ et $z’ := \frac{z \, Z}{z + Z}$, ce qui ne saute pas exactement aux yeux quand on considère les deux objets en coordonnées usuelles. Inversement, un équilibreur zigzag avec les paramètres $Z’$ et $z’$ est équivalent à une charge couplée étoile-triangle avec les paramètres $Z := 3 Z’ + z’$ et $z = z’ (1 + \frac{z’}{3 Z’})$. Cette démonstration de l’identité entre deux composants d’apparence différente est une belle illustration de la puissance de la théorie des composantes symétriques.