Remarque : Les lignes électriques, de manière générale, sont généralement réputées effectivement symétriques. Certains cas de figure font cependant exception, par exemple les réseaux à moyenne tension nord-américains pour lesquels on utilise une artère principale triphasée et seulement deux phases pour les branches latérales; ces branches latérales ne sont alors évidemment pas symétriques, pas plus que les réseaux basse tension qu’elles alimentent. La technologie « Single-Wire Earth-Retun » (SWER), parfois utilisée en basse tension, est un autre exemple de situation où une ligne électrique ne possède manifestement pas la propriété de symétrie requise dans ce chapitre.
4.2.1 Ligne équilibrée simple à trois conducteurs
On considère une ligne composée de trois conducteurs identiques, chacun modélisé par une impédance propre \(Z\) et par une impédance mutuelle (soit \(j \omega\) fois l’inductance mutuelle) \(M\) avec chaque autre conducteur. On note de la façon habituelle les grandeurs associées à la première extrémité de la ligne, avec un prime les grandeurs associées à son autre extrémité.Mise en équations en coordonnées usuelles
Les équations du système, sous forme matricielle par blocs, sont les suivantes : \begin{equation} \begin{cases} V_{ABC} – V’_{ABC} = \mathcal{Z} \, I_{ABC}\\ I_{ABC} + I’_{ABC} = 0, \end{cases} \end{equation} où $$ \mathcal{Z} = \begin{bmatrix} Z & M & M\\ M & Z & M\\ M & M & Z \end{bmatrix} = Z \, I_3 + M \, (S + S^\top).$$ Le problème comporte 12 variables qui forment 4 triplets de variables triphasées, sans aucune variable isolée, et qui sont toutes des variables de ports. Il comporte par ailleurs 6 équations indépendantes réparties en 2 blocs triphasés d’équations, sans aucune équation isolée. Le composant possède donc 6 degrés de liberté, comme on s’y attend pour un composant à 6 ports. Les sous-matrices $3 \times 3$ qui interviennent dans le système d’équations sont $I_3$ et $\mathcal{Z}$ qui sont toutes les deux des matrices circulantes. La matrice du problème possède donc la structure circulante. Enfin, toutes les sous-matrices $3 \times 3$ qui interviennent dans le problème vérifient $\beta = \gamma$ au sens de la Remarque 4 : on s’attend donc à ce que les schémas direct et inverse soient identiques.Changement de base sur les triplets de variables triphasées
On effectue le changement de variables: \begin{equation} \begin{cases} F \, V_{0id} – F \, V’_{0id} = (Z \, I_3 + M \, (S + S^\top)) \, F \, I_{0id}\\ F \, I_{0id} + F \, I’_{0id} = 0. \end{cases} \end{equation}Changement de base sur les blocs triphasés d’équations
On prémultiplie ensuite par $F^{-1}$ pour obtenir: \begin{equation} \begin{cases} V_{0id} – V’_{0id} = F^{-1} \, (Z \, I_3 + M \, (S + S^\top)) \, F \, I_{0id}\\ I_{0id} + I’_{0id} = 0. \end{cases} \end{equation} Tous calculs faits, on peut rassembler en trois groupes; un système direct \begin{equation} \begin{cases} V_d – V’_d = (Z – M) I_d \\ I_d + I_d’ = 0, \end{cases} \end{equation} un système inverse \begin{equation} \begin{cases} V_i – V’_i = (Z – M) I_i \\ I_i + I_i’ = 0 \end{cases} \end{equation} et un système homopolaire \begin{equation} \begin{cases} V_0 – V’_0 = (Z + 2 M) I_0 \\ I_0 + I_0′ = 0. \end{cases} \end{equation} Les systèmes direct et inverse sont bien identiques, comme attendu.Schéma électrique symétrique
On peut interpréter ces trois systèmes d’équations découplés comme une impédance équivalente (dite « impédance cyclique ») de valeur $Z – M$ située entre les ports $(V_d, I_d)$ et $(V’_d, I’_d)$; une impédance de même valeur $Z – M$ située entre les ports $(V_i, I_i)$ et $(V’_i, I’_i)$; et une impédance de valeur $Z + 2 M$ située entre les ports $(V_0, I_0)$ et $(V’_0, I’_0)$. Notre modèle de ligne simple, exprimé en coordonnées symétriques, est donc équivalent au schéma de la figure ci-dessous.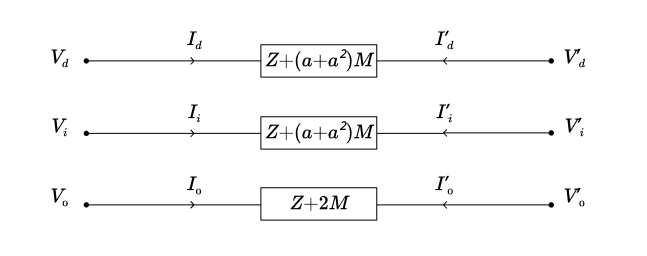
Remarque : Les formules des impédances symétriques $Z_i$ et $Z_d$ méritent qu’on prenne un instant pour s’interroger sur le signe de leur partie réelle et de leur partie imaginaire. L’impédance mutuelle $M$ est a priori purement imaginaire avec une partie imaginaire positive. L’impédance directe $Z-M$ aura ainsi pour partie réelle la résistance $R$ qui apparaît sur chaque phase dans le modèle classique, ce qui n’appelle pas de commentaire particulier, et pour partie imaginaire quelque chose d’inférieur à l’impédance $j \omega L$ qui apparaît sur chaque phase dans le modèle en coordonnées usuelles. L’effet de la présence des deux autres phases est donc de réduire l’effet inductif série, par rapport au cas d’un conducteur isolé.
4.2.2 Ligne équilibrée simple à quatre conducteurs
On considère une ligne composée de trois conducteurs de phases identiques et d’un conducteur de neutre potentiellement différent. On introduit des impédances propres $Z$ sur les phases et $z$ sur le neutre, et des impédances mutuelles (soit $j \omega$ fois l’inductance mutuelle) $M$ entre chaque paire de conducteurs de phases, et $m$ entre le neutre et une phase. On note de la façon habituelle les grandeurs associées à la première extrémité de la ligne, avec un prime les grandeurs associées à son autre extrémité.
Mise en équations en coordonnées usuelles
Les équations du système, sous forme matricielle par blocs, sont les suivantes:
\begin{equation}
\begin{cases}
V_{ABC} – V’_{ABC} = \mathcal{Z} \, I_{ABC} + m \, \un \, I_N \\
V_N – V’_N = m \, \un^\top I_{ABC} + z \, I_N\\
I_{ABC} + I’_{ABC} = 0 \\
I_N + I’_N = 0.
\end{cases}
\end{equation}
Le problème comporte 16 variables réparties en 4 triplets triphasés de variables et 4 variables isolées, et qui sont toutes des variables de ports. Il compte par ailleurs 8 équations réparties en 2 blocs triphasés d’équations et 2 équations isolées. Le composant possède donc 8 degrés de liberté, comme on s’y attend pour un composant à 8 ports.
Les sous-matrices $3 \times 3$ qui apparaissent dans le système sont $I_3$ et $\mathcal{Z}$, qui sont circulantes. Dans le premier bloc triphasé d’équation, la sous-matrice associée à la variable isolée $I_N$ est égale $m \, \un$, et le deuxième bloc triphasé d’équation n’implique aucune variable isolée. Dans la première équation isolée, la ligne associée au triplet triphasé $I_{ABC}$ est égale à $m \, \un^\top$, tandis que la deuxième équation isolée ne fait intervenir aucun triplet triphasé. La matrice possède donc la structure circulante.
Enfin, toutes les sous-matrices $3 \times 3$ qui interviennent dans le problème vérifient $\beta = \gamma$ au sens de la Remarque 4 : on s’attend donc à ce que les schémas direct et inverse soient identiques.
Changement de base sur les triplets de variables triphasées
On effectue le changement de variables, directement par des calculs matriciels:
\begin{equation}
\begin{cases}
F \, V_{0id} – F \, V’_{0id} = \mathcal{Z} \, F \, I_{0id} + m \, \un \, I_N \\
V_N – V’_N = m \, \un^\top F \, I_{0id} + z \, I_N\\
I_{0id} + I’_{0id} = 0 \\
I_N + I’_N = 0.
\end{cases}
\end{equation}
Changement de base sur le bloc triphasé d’équations
On prémultiplie le bloc triphasé d’équations par $F^{-1}$:
\begin{equation}
\begin{cases}
V_{0id} – V’_{0id} = F^{-1} \, \mathcal{Z} \, F \, I_{0id} + m \, F^{-1} \, \un \, I_N \\
V_N – V’_N = m \, \un^\top F \, I_{0id} + z \, I_N\\
I_{0id} + I’_{0id} = 0 \\
I_N + I’_N = 0.
\end{cases}
\end{equation}
La matrice $\mathcal{Z}$ a déjà été diagonalisée dans la section 4.2.1 précédente. On obtient:
\begin{equation}
\begin{cases}
V_d – V’_d = (Z + (a+a^2) M) I_d \\
V_i – V’_i = (Z + (a+a^2) M) I_i \\
V_0 – V’_0 = (Z + 2M) I_0 + m I_N \\
V_N – V’_N = 3 m I_0 + z \, I_N\\
I_{0id} + I’_{0id} = 0 \\
I_N + I’_N = 0
\end{cases}
\end{equation}
qui, pour ce qui concerne les systèmes direct et inverse, se décompose de la même manière que dans le cas d’une ligne à trois conducteurs, soit pour mémoire
\begin{equation}
\begin{cases}
V_d – V’_d = (Z – M) I_d \\
I_d + I_d’ = 0,
\end{cases}
\end{equation}
pour le système direct, et
\begin{equation}
\begin{cases}
V_i – V’_i = (Z – M) I_i \\
I_i + I_i’ = 0,
\end{cases}
\end{equation}
pour le système inverse; tandis que pour le système homopolaire, on obtient
\begin{equation}
\begin{cases}
V_0 – V’_0 = (Z + 2M) I_0 + 3 m \tilde{I}_N \\
I_0 + I’_0 = 0 \\
V_N – V’_N = 3 m I_0 + 3 z \, \tilde{I}_N\\
\tilde{I}_N + \tilde{I}’_N = 0.
\end{cases}
\end{equation}
Le système direct et le système inverse sont identiques, comme attendu.
Schéma électrique symétrique
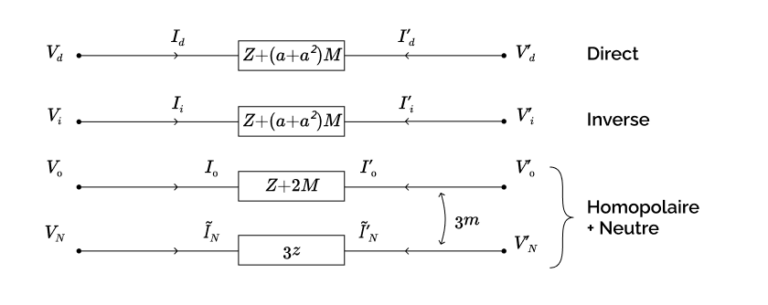
Le circuit équivalent est présenté sur la figure ci-dessous. On observe qu’il n’est pas tout à fait aussi simple que ceux que nous avons rencontrés jusqu’à présent: il reste ici une mutuelle entre le conducteur homopolaire et le conducteur de neutre.
Remarque : Le changement de variable $I_N \longrightarrow \tilde{I}_N$ nous conduit à multiplier par $3$ l’impédance du conducteur de neutre d’une ligne dans les schémas faisant intervenir $\tilde{I}_N$, par rapport à ceux faisant intervenir $I_N$. On ne doit donc pas s’étonner de voir le conducteur de neutre être modélisé par une impédance de valeur $3z$ sur le schéma de la Figure 4.1.4. L’effet serait le même pour un conducteur de mise à la terre.
4.2.3 Ligne équilibrée à trois conducteurs avec couplages capacitifs entre conducteurs
Ce cas peut être ramené à celui d’une charge (capacitive) en triangle équilibrée, suivie d’une ligne simple à trois conducteurs, suivie d’une autre charge (capacitive) en triangle équilibrée.
4.2.4 Ligne équilibrée à quatre conducteurs avec couplages capacitifs entre conducteurs
Ce cas peut être ramené à celui d’une charge (capacitive) en triangle équilibrée, suivie d’une charge (capacitive) en étoile équilibrée à neutre relié, suivie d’une ligne à quatre conducteurs, suivie d’une charge (capacitive) en étoile équilibrée à neutre relié, suivie d’une charge (capacitive) en triangle équilibrée.
4.2.5 Ligne à trois conducteurs avec couplage à la terre
On ajoute maintenant les éléments transverses vers la terre; et on conserve, si on le souhaite, les couplages capacitifs entre conducteurs, qui forment une charge triangle de chaque côté de la ligne et que l’on peut modéliser séparément.
Quelle différence cela fait-il avec le cas de ligne à 4 conducteurs que nous venons d’étudier? Que le courant passe dans le neutre ou dans la terre, est-ce que ça change vraiment quelque chose?
- Premièrement, on ne tient généralement pas compte d’une éventuelle inductance mutuelle entre les phases et la terre, alors qu’on le fait (parfois) entre les phases et le neutre.
- Deuxièmement, la terre profonde est généralement considérée comme parfaitement conductrice. Elle ne doit donc pas être modélisée par une ligne mais par un simple nœud. Enfin, entre cette terre profonde parfaitement conductrice et les éléments du réseau qui y sont reliés, on introduit généralement une impédance de mise à la terre.
Nous proposons l’introduction de deux nœuds séparés, l’un à l’entrée de la ligne et un à la sortie, où se rejoindront les éléments transverses qui modélisent le couplage entre la ligne et la terre. En pratique, ces deux éléments seront certainement toujours connectés (entre eux et) à un même nœud spécifique représentant la terre profonde. La situation est représentée sur la figure ci-dessous, où les deux nœuds supplémentaires sont notés respectivement « T » au primaire et « t » au secondaire.
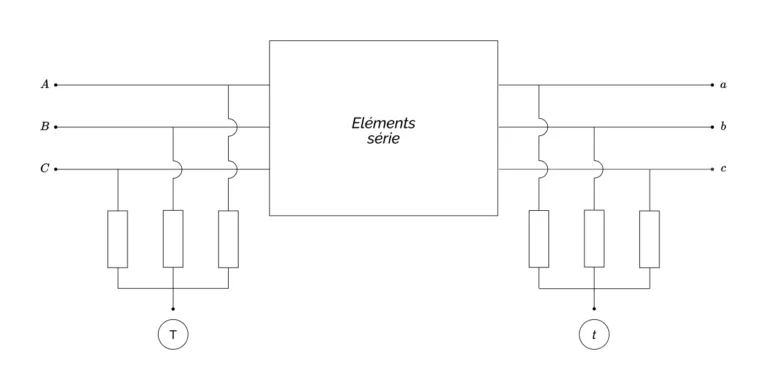
Les deux nœuds que nous venons d’introduire constituent en fait deux nouveaux points neutres. Notre modèle est donc identique à celui de la ligne à trois conducteurs précédée et suivie d’une charge étoile, les deux points neutres ainsi créés étant destinés à être reliés à un nœud de terre commun à l’ensemble du réseau.
4.2.6 Ligne à quatre conducteurs avec couplages capacitifs entre conducteurs et couplage à la terre
On cumule: une charge triangle pour les couplages capacitifs entre phases, une charge étoile à neutre relié pour les couplages capacitifs entre phase et neutre, une charge étoile à neutre non-relié pour les éléments transverses de couplage avec la terre, puis une ligne simple à 4 conducteurs, et enfin, de nouveau tous les mêmes composants qu’en début de ligne.
Remarque : Tous les types de lignes symétriques que nous venons de décrire sont des cas particuliers du modèle le plus complet, celui de la ligne à quatre conducteurs avec couplages capacitifs entre conducteurs et couplage à la terre. On peut donc considérer que nous n’avons en fait introduit qu’un seul modèle de ligne.
4.2.7 Agrégation de lignes successives
Lorsque deux lignes sans éléments transversaux se succèdent, et qu’il n’y a pas de charge ni d’éléments transverses (entre conducteurs ou avec la terre) à leur point de connexion, ces lignes peuvent être agrégées par sommation de leurs impédances symétriques comme indiqué sur la figure ci-dessous pour le cas d’une ligne à 3 conducteurs. Comme nous le verrons dans le chapitre 5, cette situation se produit notamment dans le cas des études de défauts, que l’on réalise souvent en négligeant les charges et en négligeant les couplages capacitifs.
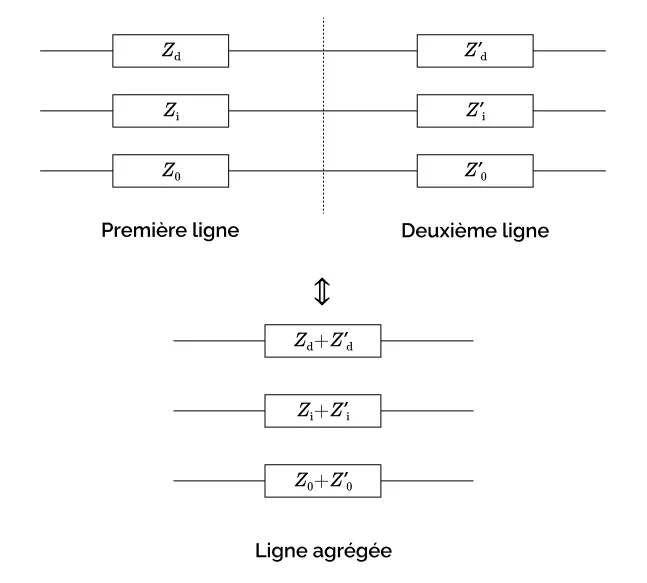
Dans le cas d’un réseau bouclé, on peut réaliser le même type d’opération sur les lignes placées en parallèle: leurs admittances symétriques s’ajoutent.
Remarque : Si nous étions restés en coordonnées usuelles, nous aurions pu tout aussi bien agréger les lignes successives de la même manière en sommant leurs impédances (propres et mutuelles) de la même manière. La possibilité d’agréger facilement des lignes entre elles n’est donc pas particulièrement un argument en faveur de la théorie des composantes symétriques.
