Nous allons maintenant étudier le cas des transformateurs triphasés, en commençant par supposer que ceux-ci sont formés d’un assemblage de trois transformateurs monophasés ; cette hypothèse nous permettra d’utiliser le modèle classique de transformateur monophasé présenté dans le Chapitre 2 et ainsi de construire le modèle du transformateur triphasé par assemblage de sous-composants déjà connus. Le cas des transformateurs triphasés à circuit magnétique unique, quant à lui, sera traité dans la partie 4.4
Remarque : Dans le modèle usuel de transformateur monophasé, le primaire et le secondaire ne jouent pas des rôles symétriques : on place traditionnellement l’impédance magnétisante au primaire, et l’impédance série au secondaire. Les modèles de transformateurs triphasés que nous allons obtenir par cette approche ne seront donc pas symétriques non plus, et seraient différents si nous inversions le sens du modèle de transformateur monophasé, ou si nous adoptions un modèle de transformateur monophasé dans lequel le primaire et le secondaire jouent des rôles symétriques.
Nous allons commencer par étudier le cas du transformateur étoile-étoile, qui constitue un cas un peu particulier, avant de nous intéresser aux autres types de couplages.
4.3.1. Transformateur étoile-étoile
Remarque : Il semble que le couplage étoile-étoile soit peu utilisé en pratique, en tout cas dans le domaine des transformateurs de puissance; nous laissons néanmoins aux spécialistes le soin de confirmer ce point.
On considère un transformateur étoile-étoile YY0 constitué de trois transformateurs monophasés identiques que nous modéliserons de façon usuelle. On note $\alpha := \frac{N}{n}$ leur rapport de transformation. Les impédances magnétisantes forment une charge étoile équilibrée, que nous allons ignorer temporairement et réintégrer en fin de calcul, de même que les impédances séries au secondaire qui forment une ligne symétrique à quatre conducteurs (avec un neutre d’impédance différente par rapport à celle des phases). Les non-idéalités ayant été ainsi écartées, il ne nous reste plus qu’à étudier le cas du transformateur étoile-étoile idéal.
Mise en équations en coordonnées usuelles
Les équations sont simplement:
\begin{equation}
\begin{cases}
V_A – V_N = \alpha (V_A’ – V_N’) \\
V_B – V_N = \alpha (V_B’ – V_N’) \\
V_C – V_N = \alpha (V_C’ – V_N’) \\
I_A’ + \alpha I_A = 0\\
I_B’ + \alpha I_B = 0\\
I_C’ + \alpha I_C = 0\\
I_A + I_B + I_C + I_N = 0 \\
I_A’ + I_B’ + I_C’ + I_N’ = 0
\end{cases}
\end{equation}
soit sous forme matricielle
\begin{equation}
\begin{cases}
V_{ABC} – V_N \, \un = \alpha (V_{ABC}’ – V_N’ \, \un) \\
I_{ABC}’ + \alpha \, I_{ABC} = 0\\
\un^\top I_{ABC} + I_N = 0 \\
\un^\top I_{ABC}’ + I_N’ = 0.
\end{cases}
\end{equation}
Le problème compte 16 variables qui sont toutes des variables de ports et qui sont réparties en 4 triplets triphasés et 4 variables isolées. Il compte par ailleurs 8 équations, répartis en 2 blocs triphasés d’équations et 2 équations isolées. La matrice possède la structure circulante, et les sous-matrices $3 \times 3$ qui y interviennent sont toutes des multiples de l’identité: on s’attend donc notamment à ce que les schémas direct et inverse soient identiques.
Changement de base sur les triplets de variables triphasées
On effectue le changement de base sur les triplets de variables triphasées:
\begin{equation}
\begin{cases}
F \, V_{0id} – V_N \, \un = \alpha (F \, V_{0id}’ – V_N’ \, \un) \\
F \, I_{0id}’ + \alpha \, F \, I_{0id} = 0\\
\un^\top F \, I_{0id} + I_N = 0 \\
\un^\top F \, I_{0id}’ + I_N’ = 0.
\end{cases}
\end{equation}
Changement de base sur les blocs triphasés d’équations
On effectue ensuite le changement de base sur les blocs triphasés d’équations:
\begin{equation}
\begin{cases}
V_{0id} – V_N \, F^{-1} \, \un = \alpha (V_{0id}’ – V_N’ \, F^{-1} \, \un) \\
I_{0id}’ + \alpha \, I_{0id} = 0\\
\un^\top F \, I_{0id} + I_N = 0 \\
\un^\top F \, I_{0id}’ + I_N’ = 0,
\end{cases}
\end{equation}
soit, tous calculs faits
\begin{equation}
\begin{cases}
V_0 – V_N = \alpha (V_0′ – V_N’) \\
V_d = \alpha V_d’ \\
V_i = \alpha V_i’ \\
I_0′ + \alpha \, I_0 = 0 \\
I_i’ + \alpha \, I_i = 0 \\
I_d’ + \alpha \, I_d = 0 \\
3 \, I_0 + I_N = 0 \\
3 \, I_0′ + I_N’ = 0.
\end{cases}
\end{equation}
Ce système se décompose en trois sous-systèmes indépendants; le système direct
\begin{equation}
\begin{cases}
V_d = \alpha V_d’ \\
I_d’ + \alpha \, I_d = 0,
\end{cases}
\end{equation}
le système inverse
\begin{equation}
\begin{cases}
V_i = \alpha V_i’ \\
I_i’ + \alpha \, I_i = 0
\end{cases}
\end{equation}
qui est bien identique au système direct, et le système homopolaire
\begin{equation}
\begin{cases}
V_0 – V_N = \alpha (V_0′ – V_N’) \\
I_0′ + \alpha \, I_0 = 0\\
I_0 + \tilde{I}_N = 0 \\
I_0′ + \tilde{I}_N’ = 0.
\end{cases}
\end{equation}
Schéma électrique symétrique
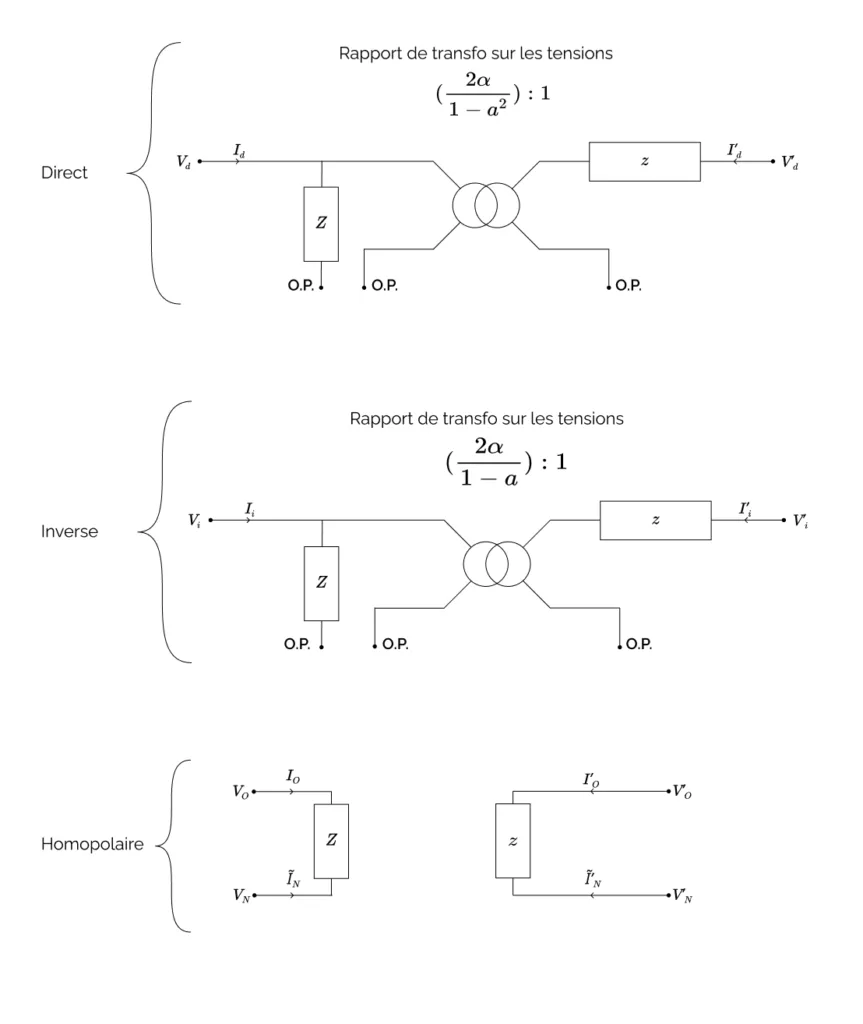
Le système direct et le système inverse peuvent être interprétés comme les deux circuits identiques qui sont représentés sur la figure ci-dessous :
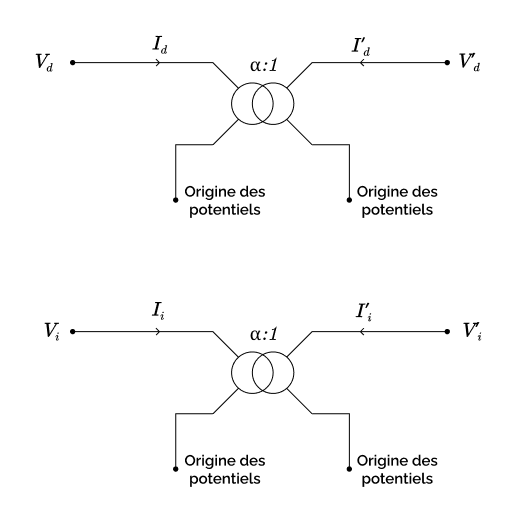
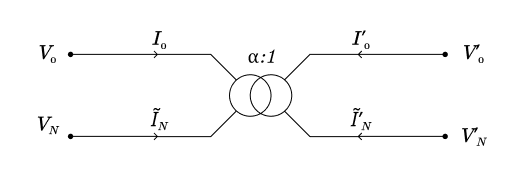
Réintégration des non-idéalités
En réintégrant les non-idéalités au primaire, où les impédances magnétisantes forment une charge étoile équilibrée, et au secondaire, où les impédances série forment une ligne équilibrée, on obtient le schéma présenté sur la figure suivante :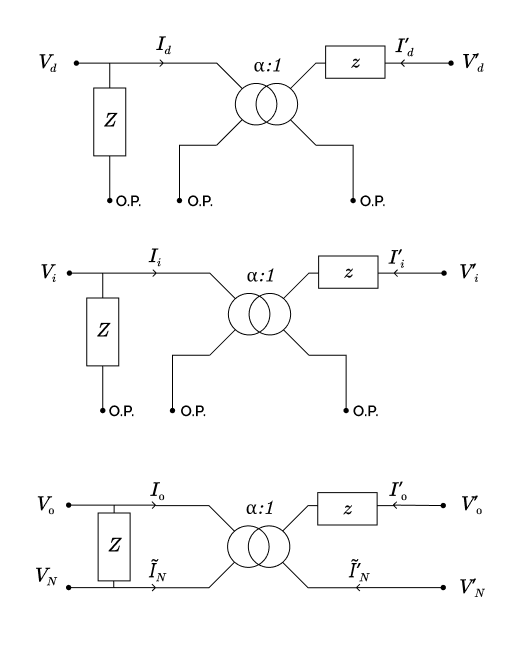
4.3.2 Transformateur triangle-étoile
On considère maintenant le transformateur triangle-étoile représenté ci-dessous, formé de trois transformateurs monophasés identiques que nous allons de nouveau modéliser en utilisant le modèle classique à deux paramètres $Z$ (impédance magnétisante) et $z$ (impédance série) qui a été présenté dans le Chapitre 2.
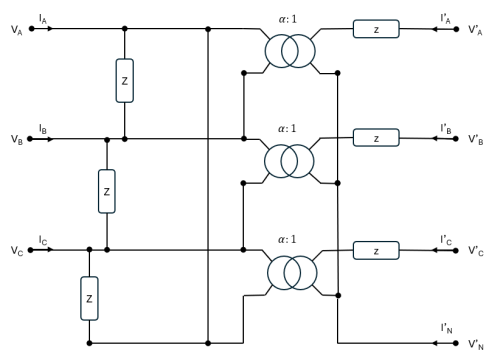
Mise en équations en coordonnées usuelles
Après avoir écarté temporairement les trois inductances magnétisantes, les équations en coordonnées usuelles sont les suivantes:
\begin{equation} \begin{cases} V_A – V_B = \alpha (V_A’ – z \, I_A’ – V_N’) \\ V_B – V_C = \alpha (V_B’ – z \, I_B’ – V_N’) \\ V_C – V_A = \alpha (V_C’ – z \, I_C’ – V_N’) \\ \alpha I_A + I_A’ = I_C’ \\ \alpha I_B + I_B’ = I_A’ \\ \alpha I_C + I_C’ = I_B’ \\ I_A’ + I_B’ + I_C’ + I_N’ = 0, \end{cases} \end{equation}soit sous forme matricielle et en réintroduisant la matrice $S$ définie par l’équation (1.3),
\begin{equation} \begin{cases} V_{ABC} – S \, V_{ABC} = \alpha (V_{ABC}’ – z \, I_{ABC}’ – V_N’ \, \un) \\ \alpha \, I_{ABC} + I_{ABC}’ = S^\top \, I_{ABC}’ \\ \un^\top \, I_{ABC}’ + I_N’ = 0. \end{cases} \end{equation}Le problème comporte 14 variables qui sont toutes des variables de ports, parmi lesquelles 4 triplets triphasés et 2 variables isolées. Il compte par ailleurs 7 équations réparties en deux blocs triphasés d’équations et une équation isolée. On vérifie facilement que la matrice possède la structure circulante.
En revanche, comme pour l’équilibreur zigzag, l’observation des sous-matrices circulantes $3 \times 3$ n’indique pas de manière évidente une similarité attendue entre les systèmes direct et inverse.
Changements de base
On effectue le changement de base sur les triplets triphasés de variables:
\begin{equation} \begin{cases} (I_3 – S) \, F \, V_{0id} = \alpha (F \, V_{0id}’ – z \, F \, I_{0id}’ – V_N’ \, \un) \\ \alpha \, F \, I_{0id} + F \, I_{0id}’ = S^\top \, F \, I_{0id}’ \\ \un^\top \, F \, I_{0id}’ + I_N’ = 0, \end{cases} \end{equation}puis le changement de base sur les deux blocs triphasés d’équations:
\begin{equation} \begin{cases} (I_3 – F^{-1} \, S \, F) \, V_{0id} = \alpha (V_{0id}’ – z \, I_{0id}’ – V_N’ \, F^{-1} \, \un) \\ \alpha \, I_{0id} + I_{0id}’ = F^{-1} \, S^\top \, F \, I_{0id}’ \\ \un^\top \, F \, I_{0id}’ + I_N’ = 0. \end{cases} \end{equation}En utilisant la formule (1.11) de diagonalisation des matrices $S$ et $S^\top$, on obtient:
\begin{equation} \begin{cases} V_0′ – V_N’ = z \, I_0′ \\ V_i = \frac{\alpha}{(1-a)} \, (V_i’ – z I_i’) \\ V_d = \frac{\alpha}{(1-a^2)} \, ( V_d’ – z I_d’) \\ I_0 = 0 \\ \alpha I_i + (1-a^2) I_i’ = 0 \\ \alpha I_d + (1-a) I_d’ = 0 \\ 3 I_0′ + I_N’ = 0. \end{cases} \end{equation}On observe bien le découplage attendu en un système direct
\begin{equation} \begin{cases} V_d = \frac{\alpha}{1-a^2} \, ( V_d’ – z I_d’) \\ I_d + \frac{1-a}{\alpha} I_d’ = 0, \end{cases} \end{equation}un système inverse
\begin{equation} \begin{cases} V_i = \frac{\alpha}{1-a} \, (V_i’ – z I_i’) \\ I_i + \frac{1-a^2}{\alpha} I_i’ = 0 \end{cases} \end{equation}et un système homopolaire, dans lequel nous effectuons le changement de variable $I_N’ \longrightarrow \tilde{I}_N’$:
\begin{equation} \begin{cases} V_0′ – V_N’ = z \, I_0′ \\ I_0′ + \tilde{I}_N’ = 0 \\ I_0 = 0. \end{cases} \end{equation}Cette fois, les équations du circuit direct et du circuit inverse ne sont pas identiques: elles sont conjuguées.
Remarque : En particulier, l’indice horaire de notre transformateur triangle-étoile, lorsqu’on l’alimente par une tension inverse, est l’opposé de l’indice horaire au sens habituel, c’est-à-dire lorsqu’on alimente notre transformateur par une tension directe.
Cette observation est en fait générale, elle s’applique à tous les transformateurs triphasés, et on peut y arriver de façon beaucoup plus simple: pour calculer l’indice horaire d’un transformateur en mode direct, on dessine un triplet triphasé direct $V_{ABC}$ dans le plan en mettant $V_A$ à midi, on détermine graphiquement $V’_A$ en utilisant la nature du couplage, et on lit l’heure indiquée par $ V’_A$. Si l’on cherche ensuite à calculer l’indice horaire de ce même transformateur en mode inverse, on fera le même raisonnement en partant cette fois d’un triplet triphasé inverse $V_{ABC}$, ce qui revient par rapport au cas précédent à permuter $V_B$ et $V_C$; par conséquent, toute la suite sera symétrique par rapport à l’axe vertical qui indique midi, et la valeur de $V_A’$ que l’on obtiendra en fin de calcul sera donc le conjugué de la valeur que nous avions obtenue dans le calcul en mode direct.
Schéma électrique
Le système d’équations direct peut être interprété comme celui du transformateur monophasé non-idéal représenté sur la figure suivante, composé d’un transformateur monophasé à rapport de transformation complexe idéal et d’une impédance $z$.
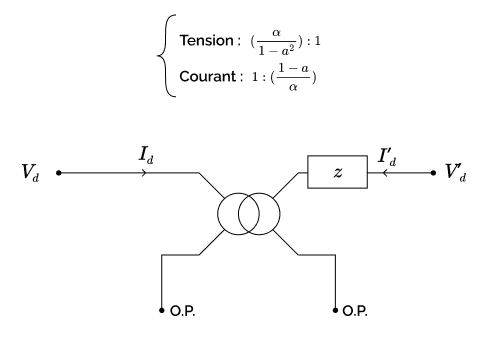
Le rapport de transformation du transformateur monophasé complexe idéal qui intervient dans le modèle est égal à
$$ \frac{\alpha}{1-a^2}. $$
L’argument du rapport de transformation complexe $\alpha/(1-a^2)$ est égal à $-\frac{\pi}{6}$. L’indice horaire est donc de 11h; c’est ce qui justifie sa dénomination de « transformateur DYn11 ».
De même, le système d’équations inverse peut être interprété comme celui du transformateur monophasé à rapport de transformation complexe idéal associé à une impédance $z$, représenté ci-dessous. Son rapport de transformation est le conjugué de celui du modèle direct.
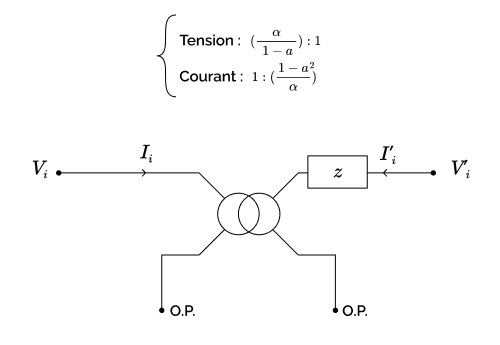
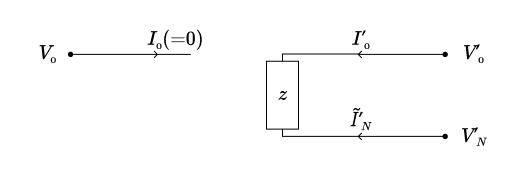
Remarque : On ne doit pas s’étonner du fait que le circuit homopolaire de notre transformateur ne comporte pas de transformateur. En effet, la circulation d’un courant homopolaire est impossible du côté du triangle, ce qui empêche tout effet d’induction magnétique entre le courant homopolaire au primaire (qui est nul) et celui au secondaire. Pour être précis, il se produit bien un effet d’induction magnétique dans l’autre sens: la circulation d’un courant homopolaire dans le secondaire couplé en étoile induira effectivement la circulation d’un courant dans le triangle au primaire (c’est précisément ce qui se passe dans le cas de la charge étoile-triangle avec secondaire à vide, que nous avons étudiée dans la partie 4.1.5); mais ce courant ne circulera alors que dans le triangle; les courants de phases ($I_0, I_0, I_0$), eux, seront nuls.
Réintégration des impédances magnétisantes
Les trois impédances magnétisantes, que nous avons pour le moment laissées de côté, forment une charge triphasée équilibrée en triangle dont nous savons qu’elle est caractérisée par les impédances directe et inverse $Z_d = Z_i = \frac{Z}{3}$, et par une admittance homopolaire nulle. Le schéma symétrique complet du transformateur triangle-étoile formé de trois transformateurs monophasés, après réintégration des impédances magnétisantes, est présenté sur la figure ci-dessous :
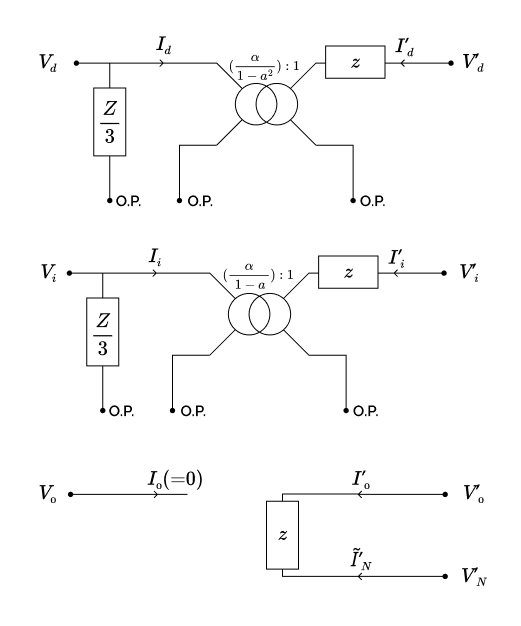
Remarque : Si les rapports de transformation complexes qui apparaissent dans le schéma direct et dans le schéma inverse ne sont pas identiques, mais conjugués comme nous l’avons déjà signalé, on observe que les impédances qui apparaissent dans ces deux circuits sont bien identiques. Nous reviendrons sur cette observation lorsque nous étudierons d’autres types de couplages.
Modélisation par la méthode des solutions particulières
Nous avions déjà illustré cette méthode de modélisation alternative en montrant, dans le cas des charges étoile et triangle équilibrées, qu’elle permettait d’aboutir de façon assez rapide à la formulation symétrique d’un modèle de composant. Illustrons de nouveau cette méthode dans le cas du transformateur triangle-étoile formé de trois transformateurs monophasés.
On commence par chercher une solution purement directe:
$$ V_{ABC} = (V_d, a^2 V_d, a V_d), \quad I_{ABC} = (I_d, a^2 I_d, a I_d), \quad \mbox{etc}. $$
On se concentre sur la phase A, sachant que la situation sera la même (au déphasage près) sur les deux autres. L’équation du transformateur monophasé pour ce qui concerne la tension, sachant que $V_N’$ est nul par hypothèse, est
$$ (1-a^2) V_d = \alpha (V_d’ -z \, I_d’). $$
Pour ce qui concerne le courant, sachant que le courant dans l’impédance magnétisante de A vers B est $\frac{1-a^2}{Z} V_d$ et le courant dans l’inductance magnétisante de A vers C est $\frac{1-a}{Z} V_d$, on a
$$ I_d = \frac{1-a^2}{Z} V_d + \frac{1-a}{Z} V_d + \frac{1}{\alpha} a I_d’ – \frac{1}{\alpha} I_d’. $$
On retrouve ainsi les mêmes équations directes qu’en passant par l’écriture du système usuel et par le changement de variables:
\begin{equation}
\begin{cases}
V_d = \frac{\alpha}{1-a^2} (V_d’ -z \, I_d’) \\
I_d = \frac{3}{Z} V_d + \frac{a-1}{\alpha} I_d’.
\end{cases}
\end{equation}
Le cas du schéma inverse est très similaire. Pour le schéma homopolaire, toujours en se concentrant sur la phase A uniquement, l’équation du transformateur monophasé pour la tension est
$$ V_0′ – z \, I_0′ – V_N’ = 0. $$
Enfin, sachant que le courant dans les inductances magnétisantes est nul, l’équation du transformateur monophasé pour le courant donne
$$ I_0 = 0 $$
et la loi des nœuds au secondaire donne enfin
$$ 3 I_0 + I_N’ = 0. $$
On retrouve bien le même système homopolaire que par la méthode classique.
4.3.3. Transformateur étoile-zigzag
Nous allons maintenant étudier un deuxième exemple de couplage: le transformateur étoile-zigzag. Ce type de transformateur est composé d’un assemblage de transformateurs monophasés à trois enroulements; pour représenter ce composant, nous adopterons le modèle présenté dans le Chapitre 2.
Mise en équations en coordonnées usuelles
Le schéma du transformateur étoile-zigzag est représenté ci-dessous.
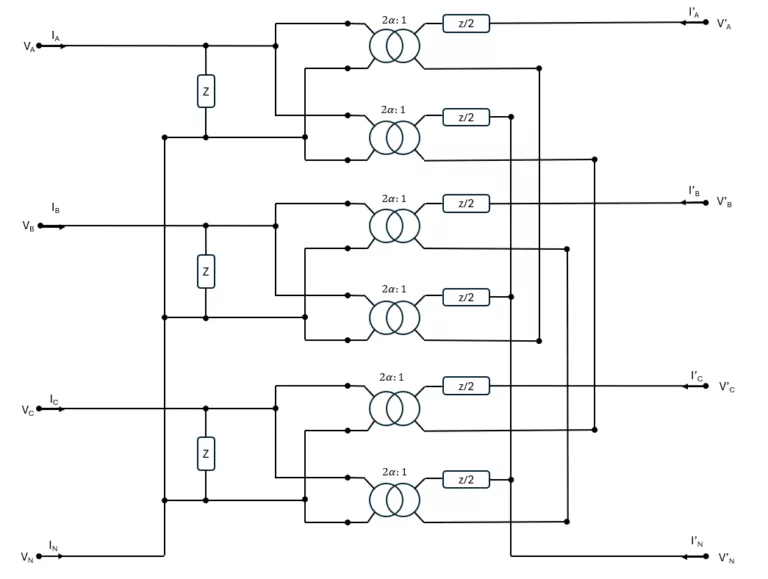
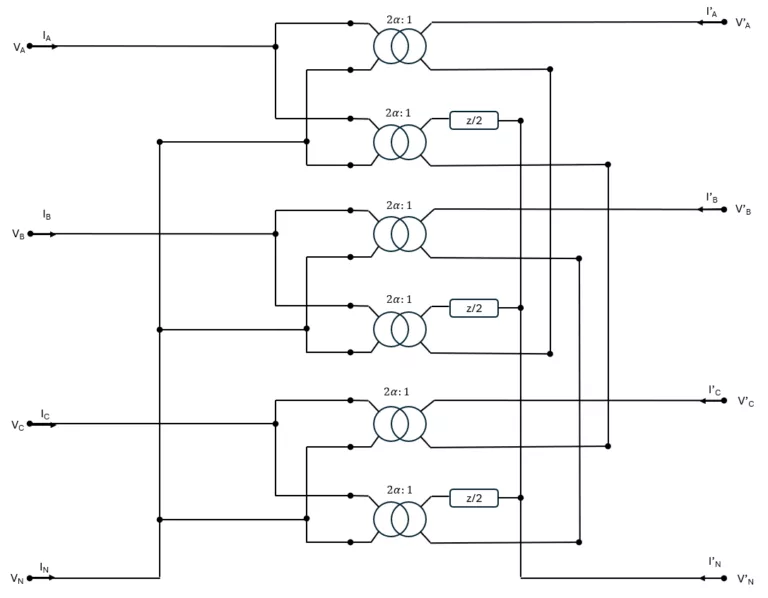
Changements de base
On effectue le changement de base sur les triplets de variables triphasées: \begin{equation} \begin{cases} F \, V_{0id}’ – V_N’ \, \un = \frac{1}{2 \alpha} (F – S \, F) \, V_{0id} + \frac{z}{2} \, F \, I_{0id}’ \\ F \, I_{0id} + \frac{1}{2 \alpha} (I_3 – S^\top) \, F \, I_{0id}’ = 0 \\ \un^\top F \, I_{0id} + I_N = 0 \\ \un^\top F \, I_{0id}’ + I_N’ = 0. \end{cases} \end{equation} On effectue ensuite le changement de base sur les blocs triphasés d’équations: \begin{equation} \begin{cases} V_{0id}’ – V_N’ \, F^{-1} \, \un = \frac{1}{2 \alpha} (I_3 – F^{-1} \, S \, F) \, V_{0id} + \frac{z}{2} \, I_{0id}’ \\ I_{0id} + \frac{1}{2 \alpha} \, (I_3 – F^{-1} \, S^\top \, F) \, I_{0id}’ = 0 \\ \un^\top F \, I_{0id} + I_N = 0 \\ \un^\top F \, I_{0id}’ + I_N’ = 0. \end{cases} \end{equation} En utilisant la formule (1.11) de diagonalisation des matrices $S$ et $S^\top$, on obtient comme attendu trois systèmes indépendants; un système direct \begin{equation} \begin{cases} V_d’ – \frac{z}{2} I_d’ = \frac{1-a^2}{2 \alpha} V_d \\ I_d = \frac{1-a}{2 \alpha} I_d’, \end{cases} \end{equation} un système inverse \begin{equation} \begin{cases} V_i’ – \frac{z}{2} I_i’ = \frac{1-a}{2 \alpha} V_i \\ I_i = \frac{1-a^2}{2 \alpha} I_i’, \end{cases} \end{equation} et un système homopolaire, dans lequel on effectue le changement de variable $I_N \longrightarrow \tilde{I}_N$ au primaire et au secondaire \begin{equation} \begin{cases} V_0′ – V_N’ = \frac{z}{2} I_0′ \\ I_0′ + \tilde{I}_N’ = 0 \\ I_0 = 0\\ \tilde{I}_N = 0. \end{cases} \end{equation} Comme attendu, le modèle direct et le modèle inverse sont conjugués l’un de l’autre. Le terme $1-a^2$ qui apparaît dans le système direct, et dont l’argument est 30°, indique de l’indice horaire de ce transformateur est 11.Schéma électrique symétrique
Le système direct peut être interprété comme les équations du circuit qui est représenté ci-dessous :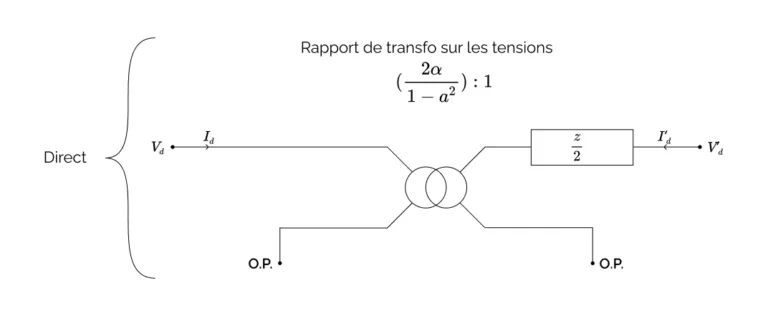
Le système inverse, comme celles du circuit qui est représenté ci-dessous :
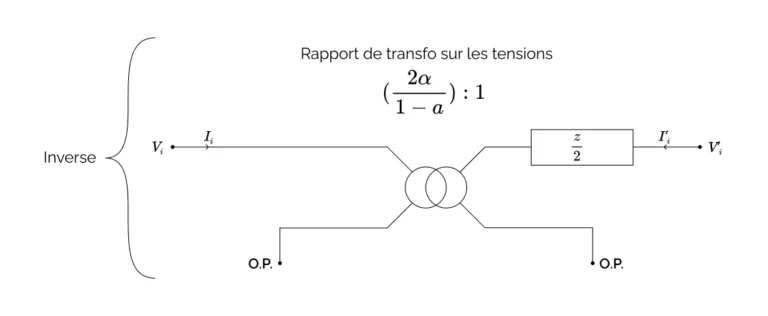
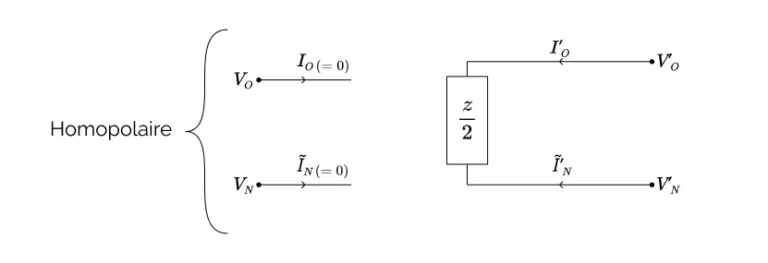
Réintégration des non-idéalités précédemment écartées
En réintégrant les impédances magnétisantes, qui forment une charge étoile en amont du primaire, et les impédances $z/2$ que nous avions considérées comme une ligne placée en aval du secondaire, le modèle symétrique complet devient celui qui est représenté ici :
Le schéma symétrique du transformateur étoile-zigzag possède donc exactement la même structure que celui du transformateur triangle-étoile, avec:
- dans le schéma direct, un modèle de transformateur monophasé à rapport de transformation complexe, non-idéal, dont le primaire est connecté entre $(V_d, I_d)$ et l’origine des potentiels, et le secondaire entre $(V_d’, I_d’)$ et l’origine des potentiels;
- un schéma inverse quasi-identique au schéma direct, la seule différence étant que le rapport de transformation du transformateur est le conjugué de celui qui apparaît dans le schéma direct (les impédances qui apparaissent dans le circuit direct et dans le circuit inverse sont en revanche identiques, exactement comme nous l’avions signalé à la Remarque 4.3.4 pour le transformateur triangle-étoile);
- un schéma homopolaire réduit à une simple impédance de chaque côté, ou éventuellement à un circuit ouvert (on parlera alors plutôt d’une admittance, en l’occurrence nulle, plutôt que d’une impédance) placée entre $(V_0, I_0)$ et $(V_N, \tilde{I}_N)$ au primaire, et $(V_0′, I_0′)$ et $(V_N’, \tilde{I}_N’)$ au secondaire.
Cette structure commune au transformateur étoile-zigzag et au transformateur triangle-étoile sera qualifiée dans la partie 4.3.4 suivante de « modèle unifié de transformateur ».
Remarque :
L’équilibreur zigzag qui a été présenté dans la partie 4.1.6 peut être modélisé par un transformateur étoile-zigzag dont seul le secondaire en zigzag est utilisé, et dont le primaire en étoile est laissé à vide. Dans ce cas, cependant, il faut prendre garde au fait que l’état électrique de l’enroulement inutilisé en étoile sera indéterminé: les équations n’imposent que la forme du triangle des potentiels de l’étoile, et pas la position du point neutre. La matrice sera donc singulière, pour une raison artificielle puisque l’indétermination ne concerne qu’une partie du circuit que l’on n’utilise pas. Il faudra donc par exemple relier le point neutre de l’étoile à l’une des phases pour lever l’indétermination, ou alors utiliser un modèle dans lequel seul le bobinage zigzag apparaît, comme nous l’avons fait dans la partie 4.1.6.
