4.4.1. Modélisation du circuit magnétique
Un transformateur triphasé à circuit magnétique unique est un objet nouveau: contrairement au transformateur triphasé composé de trois transformateurs monophasés, on ne peut pas le décrire comme un simple assemblage de composants déjà connus. Pour le modéliser, nous devons donc revenir à la physique de son circuit magnétique, comme nous l’avons fait dans la partie 4.1.7 pour l’équilibreur étoile. Nous pourrons ensuite éliminer les variables et les paramètres magnétiques, cf la Remarque 45, pour revenir à un modèle purement électrique. C’est ce que nous allons faire dans cette partie, en nous limitant à six bobinages; ceci nous permettra de modéliser des couplages en étoile et en triangle. L’utilisation du couplage zig-zag, en revanche nécessite la modélisation d’un circuit magnétique unique supportant 9 (étoile-zigzag, triangle-zigzag) voire 12 (zigzag-zigzag) bobinages distincts, deux cas qu’il faudrait traiter séparément; nous ne le ferons pas dans cet ouvrage.
Nous appliquerons ensuite ce modèle général à l’étude de quelques couplages particuliers (étoile-étoile, triangle-étoile) que nous avons déjà étudiés dans la partie 4.3.2 dans le cas de trois circuits magnétiques séparés.
On conserve les mêmes notations que dans la partie 4.1.7, en introduisant un deuxième bobinage sur chacune des trois colonnes principales, et en introduisant une quatrième colonne au circuit magnétique. Cette modélisation permet de capturer à la fois les circuits à quatre colonnes, les circuits à 5 colonnes en mettant en parallèle les réluctances des deux colonnes supplémentaires pour n’en former qu’une seule et se ramener ainsi au cas précédent; et enfin, le cas des circuits à trois colonnes, en faisant tendre vers l’infini la réluctance de la quatrième colonne. On considère que la réluctance de fuite est la même pour les bobinages primaires et les bobinages secondaires; cette hypothèse n’a en fait pas grande importance car la valeur des ces réluctances de fuite n’est pas connue a priori et on ne l’utilise jamais. Comme nous l’avons vu pour l’équilibreur étoile, cette réluctance inconnue conduira simplement à l’apparition dans le modèle d’une certaine inductance de fuite, qui sera caractérisée par des essais sur le transformateur une fois que nous l’aurons construit; cf la Remarque 45. Comme dans la partie 4.1.7 consacrée à l’équilibreur étoile, on commence par ignorer les pertes fer; celles-ci seront intégrées au modèle ultérieurement.
La situation est représentée ci-dessous :
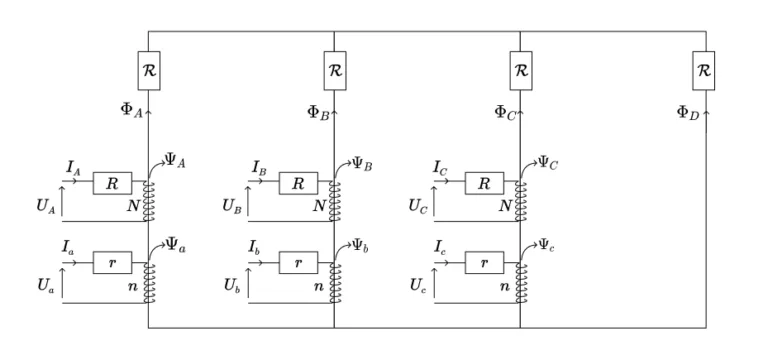
Les équations sont les suivantes.
\begin{equation}
\begin{cases}
U_A = R \, I_A + j \omega N (\phi_A + \phi^f_A) \\
U_B = R \, I_B + j \omega N (\phi_B + \phi^f_B) \\
U_C = R \, I_C + j \omega N (\phi_C + \phi^f_C)\\
U_a = r \, I_a + j \omega n (\phi_A + \phi^f_a) \\
U_b = r \, I_b + j \omega n (\phi_B + \phi^f_b) \\
U_c = r \, I_c + j \omega n (\phi_C + \phi^f_c) \\
N \, I_A + n I_a – \R \, \phi_A = – \R_D \, \phi_D\\
N \, I_B + n I_b – \R \, \phi_B = – \R_D \, \phi_D\\
N \, I_C + n I_c – \R \, \phi_C = – \R_D \, \phi_D\\
\phi_A + \phi_B + \phi_C + \phi_D = 0\\
N \, I_A – \R^f \, \phi^f_A = 0\\
N \, I_B – \R^f \, \phi^f_B = 0\\
N \, I_C – \R^f \, \phi^f_C = 0\\
n \, I_a – \R^f \, \phi^f_a = 0\\
n \, I_b – \R^f \, \phi^f_b = 0\\
n \, I_c – \R^f \, \phi^f_c = 0,
\end{cases}
\end{equation}
où $\alpha$ est la chute de force magnéto-motrice (identique) sur chacune des trois colonnes, soit sous forme matricielle
\begin{equation}
\begin{cases}
U_{ABC} = R \, I_{ABC} + j \omega N (\phi_{ABC} + \phi^f_{ABC}) \\
U_{abc} = r \, I_{abc} + j \omega n (\phi_{ABC} + \phi^f_{abc}) \\
N I_{ABC} + n I_{abc} – \R \, \phi_{ABC} = -\R_D \, \phi_D \, \un \\
\un^\top \phi_{ABC} + \phi_D = 0\\
N \, I_{ABC} – \R^f \, \phi^f_{ABC} = 0 \\
n \, I_{abc} – \R^f \, \phi^f_{abc} = 0.
\end{cases}
\end{equation}
Sachant que les tensions $U$ comptent pour deux potentiels, notre composant compte 12 variables de potentiels. Il compte également 6 variables de courant, 4 variables de flux dans les colonnes et 6 variables de flux de fuite, soit au total 28 variables. Il comporte par ailleurs 16 équations, soit 12 degrés de liberté comme on s’y attend pour un composant à 12 ports.
Les variables de flux de fuite peuvent être éliminées trivialement grâce aux six dernières équations; quant aux quatre équations précédentes, elles nous permettent d’éliminer les variables de flux dans les colonnes du circuit magnétiques au prix de quelques calculs par blocs qui donnent
\begin{equation}
\label{eq:phi-fonction-de-fmm-totale-transfo-CM-unique}
\begin{split}
\phi_{ABC} &= \Big(\Y \, I_3 – \frac{\Y^2}{3 \Y + \Y_D} \un \un^\top \Big) (N \, I_{ABC} + n \, I_{abc}) \\
&= K \, (N \, I_{ABC} \, + \, n \, I_{abc})
\end{split}
\end{equation}
où l’on a introduit la matrice
\begin{equation}
\label{eq:K-circuit-magnetique-unique}
\begin{split}
K &:= \Y \, I_3 – \frac{\Y^2}{3 \Y + \Y_D} \un \un^\top \\
&= \frac{\Y}{3 \Y + \Y_D} ((2 \Y + \Y_D) \, I_3 – \Y (S + S^\top)),
\end{split}
\end{equation}
et
$$ \phi_D = – \frac{\Y \Y_D}{3 \Y + \Y_D} \, (N \un^\top I_{ABC} + n \un^\top I_{abc}). $$
Après ces simplifications, les équations de notre composant deviennent:
\begin{equation}
\begin{cases}
U_{ABC} = ((R + j \omega N^2 \Y^f) I_3 + j \omega N^2 K) \, I_{ABC} + j \omega n N K \, I_{abc} \\
U_{abc} = ((r + j \omega n^2 \, \Y^f) I_3 + j \omega n^2 K) \, I_{abc} + j \omega n N K \, I_{ABC}.
\end{cases}
\end{equation}
On effectue ensuite le changement de variables:
\begin{equation}
\begin{cases}
F \, U_{ZID} = ((R + j \omega N^2 \Y^f) I_3 + j \omega N^2 K) \, F \, I_{ZID} + j \omega n N K \, F \, I_{0id} \\
F \, U_{0id} = ((r + j \omega n^2 \, \Y^f) I_3 + j \omega n^2 K) \, F \, I_{0id} + j \omega n N K \, F \, I_{ZID},
\end{cases}
\end{equation}
puis le changement d’équations
\begin{equation}
\begin{cases}
U_{ZID} = F^{-1} \, ((R + j \omega N^2 \Y^f) I_3 + j \omega N^2 K) \, F \, I_{ZID} + j \omega n N \, (F^{-1} \, K \, F) \, I_{0id} \\
U_{0id} = F^{-1} \, ((r + j \omega n^2 \, \Y^f) I_3 + j \omega n^2 K) \, F \, I_{0id} + j \omega n N \, (F^{-1} \, K \, F) \, I_{ZID}.
\end{cases}
\end{equation}
En s’appuyant sur \eqref{eq:K-circuit-magnetique-unique} et sur (1.11), on obtient
\begin{equation}
F^{-1} \, K \, F = \Y \, \Delta
\end{equation}
où l’on a introduit la matrice
\begin{equation}
\Delta :=
\begin{bmatrix}
\frac{\Y_D}{3 \Y + \Y_D} & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{equation}
Notre système découplé s’écrit donc
\begin{equation}
\begin{cases}
U_Z = (R + j \omega N^2 \Y^f + j \omega N^2 \Y \frac{\Y_D}{3 \Y + \Y_D}) I_Z + j \omega n N \Y \frac{\Y_D}{3 \Y + \Y_D} I_0\\
U_0 = (r + j \omega n^2 \Y^f + j \omega n^2 \Y \frac{\Y_D}{3 \Y + \Y_D}) I_0 + j \omega n N \Y \frac{\Y_D}{3 \Y + \Y_D} I_Z
\end{cases}
\end{equation}
pour le système homopolaire,
\begin{equation}
\begin{cases}
U_I = (R + j \omega N^2 \Y^f + j \omega N^2 \Y) I_I + j \omega n N \Y I_i\\
U_i = (r + j \omega n^2 \Y^f + j \omega n^2 \Y ) I_i + j \omega n N \Y I_I
\end{cases}
\end{equation}
pour le système inverse, et
\begin{equation}
\begin{cases}
U_D = (R + j \omega N^2 \Y^f + j \omega N^2 \Y) I_D + j \omega n N \Y I_d\\
U_d = (r + j \omega n^2 \Y^f + j \omega n^2 \Y ) I_d + j \omega n N \Y I_D.
\end{cases}
\end{equation}
pour le système direct.
Remarque : Le paramètre $\Y_D$ qui caractérise la quatrième colonne n’intervient pas dans les équations inverse et directe. Ceci n’est pas surprenant: en effet, en régime purement direct ou purement inverse, la somme des flux dans les trois colonnes principale est nulle, et le flux dans la quatrième colonne est donc également nul. Cette dernière ne joue donc aucun rôle est ses caractéristiques physiques n’importent pas.
Pour alléger les écritures, on introduit
\begin{equation}
\begin{cases}
L := N^2 \Y \\
L’ := N^2 \Y \frac{\Y_D}{3 \Y + \Y_D} \\
L^f := N^2 \Y^f \\
l^f := n^2 \Y^f,
\end{cases}
\end{equation}
et on note toujours $\alpha := \frac{N}{n}$.
Le système homopolaire devient
\begin{equation}
\begin{cases}
U_Z = (R + j \omega L^f + j \omega L’) I_Z + \frac{1}{\alpha} (j \omega L’) I_0\\
U_0 = (r + j \omega l^f + \frac{j \omega L’}{\alpha^2}) I_0 + \frac{1}{\alpha} (j \omega L’) I_Z
\end{cases},
\end{equation}
tandis que le système inverse devient
\begin{equation}
\begin{cases}
U_I = (R + j \omega L^f + j \omega L) I_I + \frac{1}{\alpha} (j \omega L) I_i\\
U_i = (r + j \omega l^f + \frac{j \omega L}{\alpha^2}) I_i + \frac{1}{\alpha} (j \omega L) I_I
\end{cases}
\end{equation}
et le système direct devient
\begin{equation}
\begin{cases}
U_D = (R + j \omega L^f + j \omega L) I_D + \frac{1}{\alpha} (j \omega L) I_d\\
U_d = (r + j \omega l^f + \frac{j \omega L}{\alpha^2}) I_d + \frac{1}{\alpha} (j \omega L) I_D
\end{cases}.
\end{equation}
En comparant ces trois jeux d’équations à 2.8, on les identifie aux trois modèles de transformateurs monophasés représentés sur les figures ci-dessous.
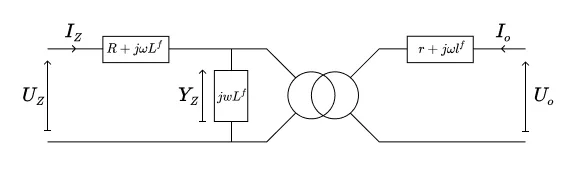
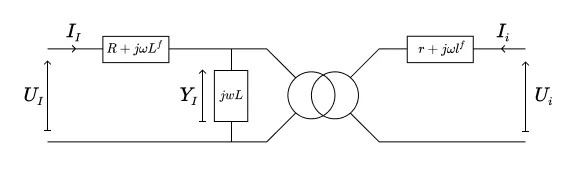
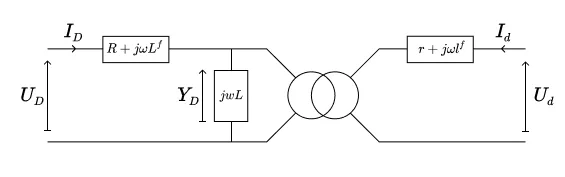
Dans le circuit homopolaire, on note $\Upsilon_Z$ la tension aux bornes de l’admittance transverse ; d’après (2.9) celle-ci est donnée par
\begin{equation}
\Upsilon_Z = \frac{j \omega L’}{N} (N I_Z + n i_0) = \frac{j \omega L}{N} \frac{\Y_D}{3 \Y + \Y_D} (N I_Z + n i_0) .
\end{equation}
De même, dans le circuit inverse, la tension $\Upsilon_I$ aux bornes de l’admittance transverse est donnée par
\begin{equation}
\Upsilon_I = \frac{j \omega L}{N} (N I_I + n i_i),
\end{equation}
et dans le circuit direct, la tension $\Upsilon_D$ aux bornes de l’admittance transverse est donnée par
\begin{equation}
\Upsilon_D = \frac{j \omega L}{N} (N I_D + n i_d).
\end{equation}
Autrement dit,
\begin{equation}
\Upsilon_{ZID} = \frac{j \omega L}{N} \, \Delta \, (N I_{ZID} + n I_{0id}),
\end{equation}
et le vecteur des trois forces magnétomotrices totales s’écrit donc
\begin{equation}
\label{eq:Upsilon-donne-fmm-totale-CM-unique}
N I_{ABC} + n i_{ABC} = F \, (N I_{ZID} + n i_{0id}) = \frac{N}{j \omega L} \, F \, \Delta^{-1} \, \Upsilon_{ZID}.
\end{equation}
D’autre part, en considérant que les trois colonnes principales du circuit magnétique sont de section $S$ et de longueur $l$ tandis que la quatrième colonne est de section $S_D$ et de longueur $l_D$, les pertes fer totales $P_f$ dans le circuit magnétique s’écrivent
\begin{equation}
\begin{split}
P_f &:= \alpha (\frac{l}{S} |\phi_{ABC}|^2 + \frac{l_D}{S_D} |\phi_D|^2) \\
&= \alpha (\frac{l}{S} |\phi_{ABC}|^2 + \frac{l_D}{S_D} |\un^\top \phi_{ABC}|^2) \\
&= \alpha (\frac{l}{S} |\phi_{ABC}|^2 + \frac{l_D}{S_D} \phi_{ABC}^{\top*} \, (\un \un^\top) \, \phi_{ABC}) \\
&= \alpha \, \phi_{ABC}^{\top*} \, (\frac{l}{S} \, I_3 + \frac{l_D}{S_D} \un \un^\top) \, \phi_{ABC}\\
&= \alpha \, (N \, I_{ABC} \, + \, n \, I_{abc})^{\top*} \, K \, (\frac{l}{S} \, I_3 + \frac{l_D}{S_D} \un \un^\top) \, K \, (N \, I_{ABC} \, + \, n \, I_{abc})\\
&= \alpha \, \frac{N^2}{(\omega L)^2}\, \Upsilon_{ZID}^{\top*} \, \Delta^{-1} \, F^{*} \, \, K \, (\frac{l}{S} \, I_3 + \frac{l_D}{S_D} \un \un^\top) \, K \, F \, \Delta^{-1} \, \Upsilon_{ZID}
\end{split}
\end{equation}
où $\alpha$ est le coefficient de pertes du matériau magnétique utilisé à la pulsation $\omega$ (cf la partie 2). L’avant-dernière égalité vient de \eqref{eq:phi-fonction-de-fmm-totale-transfo-CM-unique} et la dernière vient de \eqref{eq:Upsilon-donne-fmm-totale-CM-unique}.
Après s’être remémoré que
$$ F^{-1} (\un \un^\top) F =
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix} =: \Delta_1,
$$
on décompose ce calcul en trois opérations de diagonalisation individuelles~:
\begin{equation}
\begin{split}
& F^{*} \, \, K \, (\frac{l}{S} \, I_3 + \frac{l_D}{S_D} \un \un^\top) \, K \, F \\
=& \, 3 (F^{-1} \, K \, F) \, (F^{-1} \, (\frac{l}{S} \, I_3 + \frac{l_D}{S_D} \un \un^\top) \, F) \, (F^{-1} \, K \, F) \\
=& \, 3 (\Y \, \Delta) \, (\frac{l}{S} \, I_3 + 3 \frac{l_D}{S_D} \Delta_1) \, (\Y \, \Delta)
\end{split}
\end{equation}
soit
\begin{equation}
\begin{split}
P_f &:= 3 \Y^2 \alpha \, \frac{N^2}{(\omega L)^2}\, \Upsilon_{ZID}^{\top*} \, (\Delta^{-1} \, \Delta) \, (\frac{l}{S} \, I_3 + 3 \frac{l_D}{S_D} \Delta_1) \, (\Delta\, \Delta^{-1}) \, \Upsilon_{ZID} \\
&= \frac{3 \alpha}{\omega^2 N^2}\, \Upsilon_{ZID}^{\top*} \, (\frac{l}{S} \, I_3 + 3 \frac{l_D}{S_D} \Delta_1) \, \Upsilon_{ZID}
\end{split}
\end{equation}
c’est-à-dire finalement
\begin{equation}
P_f = \frac{3 \alpha}{\omega^2 N^2}\, \Big( (\frac{l}{S} + 3 \frac{l_D}{S_D}) |\Upsilon_Z|^2 + \frac{l}{S} |\Upsilon_I|^2 + + \frac{l}{S} |\Upsilon_D|^2 \Big).
\end{equation}
Ces pertes sont égales à celles que produiraient trois résistances de valeur
\begin{equation}
R_Z := \frac{\omega^2 N^2}{3 \alpha} \frac{1}{\frac{l}{S} + 3 \frac{l_D}{S_D}}, \quad R_I := \frac{\omega^2 N^2 S}{3 \alpha l} \quad \mbox{et} \quad R_D := R_I
\end{equation}
respectivement soumises aux tensions $\Upsilon_Z$, $\Upsilon_I$ et $\Upsilon_D$. Ceci justifie le fait de modéliser les pertes fer par l’introduction de ces trois résistances en parallèle de l’admittance transverse dans les circuits des trois figures précédentes.
Avec cette modification, le système homopolaire devient
\begin{equation}
\begin{cases}
U_Z = (R + j \omega L^f + \Lambda_Z) I_Z + \frac{1}{\alpha} \Lambda_Z I_0\\
U_0 = (r + j \omega l^f + \frac{\Lambda_Z}{\alpha^2}) I_0 + \frac{1}{\alpha} \Lambda_Z I_Z
\end{cases},
\end{equation}
où l’on a introduit
$$ \Lambda_Z := (j \omega L’) // R_Z = \frac{(j \omega L’) \, R_Z}{j \omega L’ + R_Z}, $$
tandis que le système inverse devient
\begin{equation}
\begin{cases}
U_I = (R + j \omega L^f + \Lambda_I) I_I + \frac{1}{\alpha} \Lambda_I I_i\\
U_i = (r + j \omega l^f + \frac{\Lambda_I}{\alpha^2}) I_i + \frac{1}{\alpha} \Lambda_I I_I
\end{cases}
\end{equation}
où l’on a introduit
$$ \Lambda_I := (j \omega L) // R_I = \frac{(j \omega L) \, R_I}{j \omega L + R_I}, $$
et le système direct devient
\begin{equation}
\begin{cases}
U_D = (R + j \omega L^f + \Lambda_D) I_D + \frac{1}{\alpha} \Lambda_D I_d\\
U_d = (r + j \omega l^f + \frac{\Lambda_D}{\alpha^2}) I_d + \frac{1}{\alpha} \Lambda_D I_D
\end{cases}
\end{equation}
où l’on a introduit
$$ \Lambda_D := \Lambda_I. $$
4.4.2 Transformateur étoile-étoile à circuit magnétique unique
Commençons par le cas particulier du transformateur étoile-étoile. Les équations de couplage des bobinages sont
\begin{equation}
\begin{cases}
V_{ABC} – \un V_N = U_{ABC} \\
\un^\top I_{ABC} + I_N = 0 \\
V_{abc} – \un V_n = U_{abc} \\
\un^\top I_{abc} + I_n = 0
\end{cases}
\end{equation}
soit
\begin{equation}
\begin{cases}
V_Z – V_N = U_Z \\
V_I = U_I \\
V_D = U_D \\
I_Z + \tilde{I}_N = 0 \\
V_0 – V_n = U_0 \\
V_i = U_i \\
V_d = U_d \\
I_0 + \tilde{I}_n = 0.
\end{cases}
\end{equation}
Les équations symétriques du transformateur étoile-étoile à circuit magnétique unique avec prise en compte des pertes fer sont donc les suivantes :
\begin{equation}
\begin{cases}
V_Z – V_N = (R + j \omega L^f + \Lambda_Z) I_Z + \frac{1}{\alpha} \Lambda_Z I_0\\
I_Z + \tilde{I}_N = 0 \\
V_0 – V_n = (r + j \omega l^f + \frac{\Lambda_Z}{\alpha^2}) I_0 + \frac{1}{\alpha} \Lambda_Z I_Z\\
I_0 + \tilde{I}_n = 0
\end{cases}
\end{equation}
pour le circuit homopolaire,
\begin{equation}
\begin{cases}
V_I = (R + j \omega L^f + \Lambda_I) I_I + \frac{1}{\alpha} \Lambda_I I_i\\
V_i = (r + j \omega l^f + \frac{\Lambda_I}{\alpha^2}) I_i + \frac{1}{\alpha} \Lambda_I I_I
\end{cases}
\end{equation}
pour le système inverse, et
\begin{equation}
\begin{cases}
V_D = (R + j \omega L^f + \Lambda_D) I_D + \frac{1}{\alpha} \Lambda_D I_d\\
V_d = (r + j \omega l^f + \frac{\Lambda_D}{\alpha^2}) I_d + \frac{1}{\alpha} \Lambda_D I_D
\end{cases}
\end{equation}
pour le système direct.
On interprète ces équations comme celles des trois circuits représentés sur les trois figures :
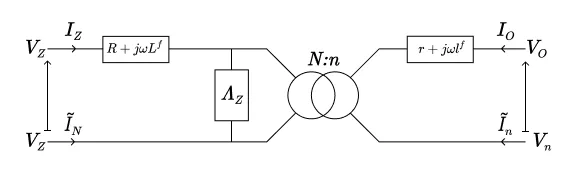
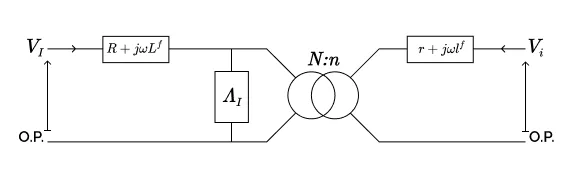
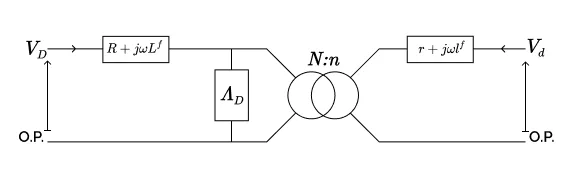
On peut éventuellement approcher ce modèle à deux impédances série par un modèle à une seule impédance série, comme dans pour le transformateur monophasé usuel (voir la partie 2).
Remarque :
Pour le modèle homopolaire, l’impédance transverse n’est pas nécessairement « grande »~; elle peut même être très petite, comme dans le cas des dispositifs équilibreurs. Il nous semble donc préférable nécessaire de conserver les deux impédances série dans le modèle (au moins dans le circuit homopolaire en tout cas), d’autant plus que cela ne le complique quand même pas excessivement.
Remarque :
On entend parfois l’idée selon laquelle un transformateur triphasé quelconque, quelle que soit la structure de son circuit magnétique, est équivalent à trois transformateurs monophasés. Cette idée est fausse comme le montre l’exemple du transformateur étoile-étoile~: lorsque celui-ci est à circuit magnétique unique à trois colonnes, il se produit (de chaque côté du transformateur) le phénomène de court-circuit homopolaire-neutre que nous avons déjà étudié dans la partie 4.1.7 consacrée à l’équilibreur étoile, tandis que ce phénomène ne se produit pas dans le transformateur étoile-étoile à flux libre et notamment dans le transformateur étoile-étoile formé de trois transformateurs monophasés. Dans notre formalisme, ceci se traduit par le fait que l’impédance transverse $\Lambda_Z$ peut être rendue très petite en rendant $L’$ très petite, c’est-à-dire en rendant $\Y_D$ très petite ou encore $\R_D$ très grand, ce qui revient à faire tendre notre circuit magnétique vers un circuit à trois colonnes. Inversement, si l’on fait tendre $\Y_D$ vers l’infini pour modéliser un transformateur à flux libre, alors $L’$ tend vers $L$ et le phénomène de court-circuit homopolaire disparaît.
4.4.3 Transformateur triangle-étoile à circuit magnétique unique
Considérons maintenant le cas du transformateur triangle-étoile. On note $I$ les courants de phase et $J$ les courants dans les bobinages. Les équations de couplage des bobinages sont
\begin{equation}
\begin{cases}
(I_3 – S) \, V_{ABC} = U_{ABC} \\
I_{ABC} = (I_3 – S^\top) \, J_{ABC} \\
V_{abc} – \un V_n = U_{abc} \\
\un^\top I_{abc} + I_n = 0
\end{cases}
\end{equation}
soit
\begin{equation}
\begin{cases}
F^{-1} \, (I_3 – S) \, F \, V_{ZID} = U_{ZID} \\
I_{ZID} = F^{-1} \, (I_3 – S^\top) \, F \, J_{ZID} \\
V_{0id} – F^{-1} \un V_n = U_{0id} \\
\un^\top F \, I_{0id} + I_n = 0
\end{cases}
\end{equation}
soit
\begin{equation}
\begin{cases}
U_Z = 0 \\
V_I (1-a) = U_I \\
V_D (1-a^2) = U_D \\
I_Z = 0 \\
I_I = (1-a^2) J_I \\
I_D = (1-a) J_D \\
V_0 – V_N = U_0\\
V_i = U_i\\
V_d = U_d\\
I_0 + \tilde{I}_n = 0.
\end{cases}
\end{equation}
Les équations symétriques du transformateur triangle-étoile à circuit magnétique unique avec prise en compte des pertes fer sont donc les suivantes. Pour le système homopolaire, on obtient
\begin{equation}
\begin{cases}
0 = (R + j \omega L^f + \Lambda_Z) J_Z + \frac{1}{\alpha} \Lambda_Z I_0\\
V_0 – V_N = (r + j \omega l^f + \frac{\Lambda_Z}{\alpha^2}) I_0 + \frac{1}{\alpha} \Lambda_Z J_Z \\
I_Z = 0\\
I_0 + \tilde{I}_n = 0.
\end{cases}
\end{equation}
soit
\begin{equation}
\begin{cases}
I_Z = 0\\
V_0 – V_N = \Sigma_0 I_0 \\
I_0 + \tilde{I}_n = 0.
\end{cases}
\end{equation}
où l’on a éliminé la variable
$$ J_Z = – \rho I_0 $$
où l’on a posé
$$ \rho := \frac{\Lambda_Z}{\alpha (R + j \omega L^f + \Lambda_Z)} $$
et
$$ \Sigma_0 := \frac{1}{\alpha^2} \, \Big( \alpha^2 (r + j \omega l^f) + \Lambda_Z – \frac{\Lambda_Z^2}{R + j \omega L^f + \Lambda_Z} \Big). $$
Le système homopolaire est donc équivalent au circuit représenté ci-dessous
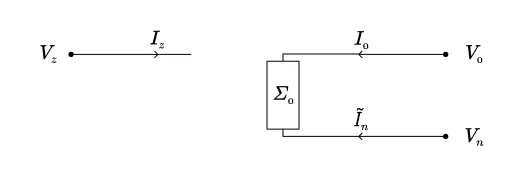
Pour le système inverse, on obtient~:
\begin{equation}
\begin{cases}
V_I = \frac{R + j \omega L^f + \Lambda_I}{3} \, I_I + \frac{\Lambda_I}{ (1-a) \alpha} I_i\\
V_i = (r + j \omega l^f + \frac{\Lambda_I}{\alpha^2}) I_i + \frac{\Lambda_I}{\alpha(1-a^2)} I_I.
\end{cases}
\end{equation}
Par comparaison avec (2.7), on identifie ce système d’équation au modèle d’un transformateur complexe non-idéal à deux impédances série, avec un rapport de transformation
$$ \mu := (1 – a^2) \, \alpha, $$
une admittance transverse
$$ Y := \frac{1}{\Lambda_I}, $$
une impédance série au primaire
$$ Z := \frac{R + j \omega L^f + \Lambda_I}{3} – \Lambda_I = \frac{R + j \omega L^f – 2 \Lambda_I}{3}, $$
et
une impédance série au secondaire
$$ z := r + j \omega l^f + \frac{\Lambda_I}{\alpha^2} – \frac{\Lambda_I}{3 \alpha^2} = r + j \omega l^f + \frac{2 \Lambda_I}{3 \alpha^2}. $$
Enfin, pour le système direct, on obtient~:
\begin{equation}
\begin{cases}
V_D = \frac{R + j \omega L^f + \Lambda_D}{3} \, I_D + \frac{1}{\alpha (1-a^2)} \Lambda_D I_d\\
V_d = (r + j \omega l^f + \frac{\Lambda_D}{\alpha^2}) I_d + \frac{\Lambda_D}{\alpha (1-a)} I_D
\end{cases}
\end{equation}
que l’on identifie de même au modèle d’un transformateur complexe non-idéal à deux impédances série, avec un rapport de transformation
$$ \mu := (1 – a) \, \alpha $$
une admittance transverse
$$ Y := \frac{1}{\Lambda_D}, $$
une impédance série au primaire
$$ Z := \frac{R + j \omega L^f + \Lambda_D}{3} – \Lambda_D = \frac{R + j \omega L^f – 2 \Lambda_D}{3}, $$
et
une impédance série au secondaire
$$ z := r + j \omega l^f + \frac{\Lambda_D}{\alpha^2} – \frac{\Lambda_D}{3 \alpha^2} = r + j \omega l^f + \frac{2 \Lambda_D}{3 \alpha^2}. $$