4.6 Modèle quasi-unifié de transformateur triphasé

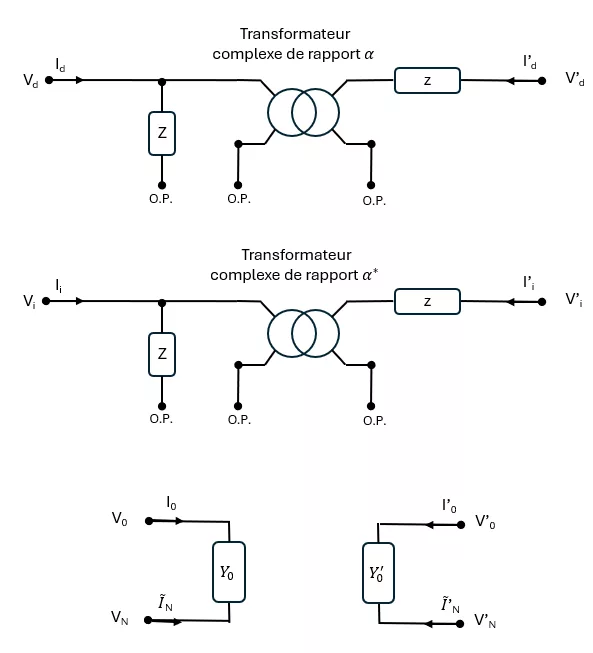
Nous allons généraliser un peu hâtivement nos observations en affirmant que ce modèle s’applique en fait à tous les couplages usuels (YY, DD, ZZ, ZD, YZ, DZ) et à tous les types de circuits magnétiques (trois circuits magnétiques séparés, ou circuit magnétique unique à 3, 4 ou 5 colonnes). Pour le démontrer de façon rigoureuse, il faudrait appliquer à tous les types de couplage la méthode que nous avons utilisée dans ce document pour traiter certains types de couplages particuliers.

Remarque : Cette affirmation fait écho à celle que nous avions faite pour les charges équilibrées en signalant que celles-ci, quelle que soit leur structure (triangle, étoile, avec ou sans couplage entre les phases…), peuvent être décrites de façon compacte et unifiée par la donnée de leurs impédances directe, inverse et homopolaire. De façon analogue, nous proposons ici grâce à la théorie des composantes symétriques un modèle quasi-unifié qui permet de décrire tous les couplages classiques de transformateurs triphasés : quelle que soit la paire de couplages retenue parmi les trois couplages usuels en étoile, en triangle et en zigzag, et quelle que soit la structure du circuit magnétique, le transformateur étudié se ramène au schéma de la figure précédente. Le modèle proposé, de plus, est beaucoup plus compact que les modèles en coordonnées usuelles dont nous sommes partis.

4.6.2 Nombre de paramètres du modèle quasi-unifié de transformateur triphasé

Dans le modèle de la figure précédente, un transformateur triphasé est caractérisé par quatre à sept grandeurs complexes selon les cas. En effet, les quatre paramètres suivants sont utilisés dans tous les cas :

• le rapport de transformation complexe direct $\mu$ (celui du système inverse sera son conjugué $\mu^*$) ;
• l’impédance transverse directe $Y$ (capturant l’inductance magnétisante et les pertes fer), qui apparaît à la fois dans le modèle direct et dans le modèle inverse ;
• l’impédance série $Z$ au primaire (capturant l’inductance de fuite et la résistance des bobinages au primaire), qui de même apparaît à la fois dans le modèle direct et dans le modèle inverse ;
• l’impédance série $z$ au secondaire (capturant l’inductance de fuite et la résistance des bobinages au secondaire), qui apparaît également à la fois dans le modèle direct et dans le modèle inverse.

Ces quatre paramètres suffisent à caractériser entièrement un transformateur triangle-triangle ; pour tous les autres types de couplages, des paramètres supplémentaires sont nécessaires :

• pour un couplage triangle-étoile ou triangle-zigzag, on doit fournir un cinquième paramètre : la valeur de l’impédance $Z’$ ou $z’$ du côté de l’étoile ou du zigzag.
• Pour un couplage étoile-zigzag ou zigzag-zigzag, on doit fournir la valeur des deux impédances $Z’$ et $z’$, ce qui nous fait passer à un modèle à six paramètres.
• Enfin, pour un couplage étoile-étoile, on doit fournir les valeurs des paramètres $Z’$, $z’$ et $Y’$, soit sept paramètres en tout dans notre modèle.

Remarque : Les deux impédances série $Z$ et $z$ peuvent éventuellement être agrégées en une seule, si l’on utilise l’approximation présentée dans le chapitre 3 ; ceci réduit à trois au lieu de quatre le nombre de paramètres complexes à fournir pour caractériser les modèles direct et inverse. De même, dans le cas du transformateur étoile-étoile, les deux impédances série $Z’$ et $z’$ peuvent éventuellement être agrégées en une seule.

Remarque : Lorsque le transformateur triphasé est constitué de trois transformateurs monophasés identiques séparés, certains des paramètres ci-dessus ne sont plus indépendants : il suffit de fournir les quatre paramètres $Z, z, Y, \mu$ du transformateur monophasé utilisé pour caractériser entièrement le transformateur triphasé.

4.6.3 Détermination de la valeur des paramètres du modèle quasi-unifié de transformateur triphasé formé de trois transformateurs monophasés

Dans le cas d’un transformateur triphasé formé de trois transformateurs monophasés identiques, il suffit de caractériser le transformateur monophasé ; on peut ensuite déterminer la caractérisation du transformateur triphasé en s’appuyant sur les formules que nous avons données dans la partie 4.3. 

Un modèle à une seule impédance série est caractérisé par son rapport de transformation réel et par deux paramètres complexes : une admittance transverse et une impédance série. On détermine traditionnellement la valeur de ces paramètres au moyen de l’essai à vide et de l’essai en court-circuit. Tout ceci est classique et nous n’entrerons pas dans les détails.

Dans le cas d’un modèle à deux impédances séries, caractérisé par son rapport de transformation (réel) et par trois paramètres complexes, il suffit de réaliser les essais plusieurs fois, en distinguant le primaire et le secondaire.

4.6.4 Détermination de la valeur des paramètres du modèle quasi-unifié de transformateur triphasé à circuit magnétique unique

Cette manière de procéder ne s’applique cependant pas au transformateur à circuit magnétique unique, qui est un objet nouveau : il nous faut donc réaliser des essais spécifiques.

4.6.4 Notion d’essai homopolaire

Outre les essais classiques à vide et en court-circuit (avec une source triphasée équilibrée directe), qui permettent de caractériser la partie directe et la partie inverse du modèle quasi-unifié de transformateur triphasé exactement comme on le ferait pour un transformateur monophasé, on doit introduire des essais supplémentaires : en effet, hormis dans le cas du transformateur triangle-triangle dont le modèle homopolaire est trivial, un à trois paramètres supplémentaires sont nécessaires pour caractériser la partie homopolaire du modèle quasi-unifié. On doit donc introduire des « essais homopolaires », similaires aux essais classiques à vide et en court-circuit mais utilisant une source homopolaire ; autrement dit, des essais réalisés avec une seule source monophasée raccordée d’un côté au point neutre et de l’autre aux trois phases raccordées entre elles. Ces essais permettent de déterminer les valeurs des impédances qui interviennent dans la partie homopolaire du modèle unifié.

4.6.4 Ersatz d’essai homopolaire

Étrangement, la pratique usuelle semble plutôt consister à ne caractériser un transformateur triphasé que par les essais à vide et en court-circuit sous tension triphasée équilibrée directe, ce qui permet de déterminer les paramètres du schéma direct du transformateur étudié ; et à supposer ensuite les autres paramètres du modèle, ceux qui interviennent dans le schéma inverse et dans le schéma homopolaire, ne sont pas indépendants et peuvent être déterminés par le calcul à partir des paramètres qui interviennent dans le système direct et par la connaissance de la nature du circuit magnétique.

De fait, généralement, les catalogues de transformateurs ne fournissent effectivement que les résultats d’essais réalisés en régime triphasé équilibré direct : on ne peut donc pas s’en servir pour caractériser la partie homopolaire du modèle quasi-unifié de transformateur. L’approche consistant à déterminer les paramètres homopolaires à partir des paramètres direct est donc souvent la seule possible en pratique, à moins de disposer d’un exemplaire physique du transformateur considéré et du matériel nécessaire pour réaliser soi-même les essais homopolaires.

L’approche consistant à supposer que les paramètres homopolaires peuvent être déterminés à partir des paramètres directs est-elle pertinente ? Cela dépend de la structure du circuit magnétique…

Pertinence de l’ersatz d’essai homopolaire dans le cas d’un transformateur triphasé formé de trois transformateurs monophasés

Considérons un transformateur triphasé formé de trois transformateurs monophasés et supposons que l’on ne dispose que des caractéristiques du transformateur triphasé, sans disposer d’essais réalisés sur le transformateur monophasé sous-jacent.

• L’hypothèse selon laquelle les paramètres du modèle inverse et du modèle homopolaire peuvent être déterminés à partir des paramètres du modèle direct, est effectivement vraie pour les transformateurs triphasés constitués de trois transformateurs monophasés que nous avons étudiés dans ce document : le transformateur triangle-étoile et le transformateur étoile-zigzag. Dans les deux cas, le modèle direct du transformateur triphasé donne la valeur des deux paramètres $Z$ et $z$ et le rapport de transformation complexe, ce qui permet de déterminer le modèle inverse (identique au modèle direct, à la conjugaison près du rapport de transformation) et le modèle homopolaire (où n’interviennent que les grandeurs $Z$ et $z$ dont le modèle direct nous a donné la valeur).
• Nous nous permettons de généraliser cette observation en affirmant qu’il en sera de même pour n’importe quel transformateur triphasé formé de trois transformateurs monophasés : le circuit homopolaire, comme l’ensemble du transformateur, ne dépend que des paramètres du transformateur monophasé sous-jacent (il n’y a pas d’autre élément constitutif !), et on sent que ces paramètres vont toujours apparaître dans le modèle direct du transformateur. On pourra donc certainement toujours déterminer les paramètres du transformateur monophasé sous-jacent à partir du modèle direct (et de la connaissance du type de couplage), puis utiliser cette information pour caractériser le modèle homopolaire.
• Généralisons encore : pour un circuit magnétique unique à flux libre, c’est-à-dire à quatre ou cinq colonnes, et dans le cas où la colonne (ou les colonnes) supplémentaire est largement dimensionnée de sorte que sa réluctance est négligeable, on revient essentiellement au cas d’un transformateur à trois circuits magnétiques séparés. De nouveau, on peut appliquer les formules comme celles des Figures 4.24 et 4.30 pour caractériser le modèle homopolaire à partir du modèle direct.

Dans ces différents cas de figure, on ne peut rien reprocher à la méthode qui consiste à déterminer l’ensemble des paramètres du modèle quasi-unifié de transformateur à partir des seuls essais à vide et en court-circuit, en régime triphasé équilibré, et de la connaissance du type de couplage. Elle revient à peu près au même que celle qui consisterait à prendre séparément l’un des trois transformateurs monophasés identiques, à le caractériser par les essais à vite et en court-circuit (monophasés), et à injecter dans le modèle triphasé les valeurs ainsi déterminées.

Pertinence de l’ersatz d’essai homopolaire dans le cas d’un transformateur triphasé à circuit magnétique unique

La situation favorable que nous venons de discuter, néanmoins, semble (très) rare en pratique : les transformateurs triphasés utilisés dans les applications réelles sont rarement composés de trois transformateurs monophasés indépendants ; et dans le cas très fréquent où le transformateur est à circuit magnétique unique, il peut très bien n’avoir que trois colonnes ; et s’il en a quatre ou cinq, il n’est pas évident que l’on puisse négliger la réluctance de la colonne (ou des colonnes) supplémentaire. Que faire ?

En désespoir de cause, des règles ad hoc, sans doute d’origine empirique, semblent être utilisées en pratique pour caractériser la partie homopolaire du modèle quasi-unifié de transformateur triphasé à partir de sa partie directe, et de la connaissance du type de couplage et de la nature du circuit magnétique (flux libre ou flux forcé).

• Lorsque le transformateur est à flux forcé et en laissant de côté le cas particulier du couplage étoile-étoile, les impédances qui apparaissent dans le modèle homopolaire peuvent être évaluées comme égales aux impédances série qui apparaissent dans le modèle direct à un certain facteur multiplicatif près (par exemple, 10 à 15 plus grandes que les impédances série du modèle direct).
• Lorsque le transformateur est à flux libre, les impédances homopolaires peuvent prendre une valeur faible ou élevée selon le type de couplage.
  • Par exemple, pour un transformateur triangle-étoile constitué de trois transformateurs monophasés, nous avons vu dans la partie 4.3.2 que l’impédance homopolaire vue du côté de l’étoile était très faible, phénomène que nous avions déjà observé en étudiant la charge couplée étoile-triangle avec secondaire à vide dans la partie 4.1.5. Dans ce cas de figure, ce n’est pas la contrainte magnétique imposée par un circuit à trois colonnes qui impose la nullité des flux magnétiques homopolaire et fait apparaître le phénomène de court-circuit homopolaire : c’est la présence de l’enroulement en triangle au secondaire, qui produit (électriquement, et non pas directement de façon magnétique) exactement le même effet. On peut alors revenir à une règle similaire à celle du transformateur à flux forcé.
  • Inversement, pour un transformateur étoile-zigzag constitué de trois transformateurs monophasés, nous avons vu dans la partie 4.3.3 que l’impédance homopolaire du côté de l’étoile était très élevée, en l’occurrence égale à l’impédance magnétisante $Z$ du transformateur monophasé sous-jacent. Il existe peut-être des règles de type « facteur multiplicatif » comme ci-dessus, mais on voit aussi des auteurs simplement considérer que l’impédance considérée est infinie (ou plus rigoureusement, que l’admittance est nulle).

Nous n’irons pas plus loin dans la discussion de ces règles ad hoc, que nous connaissons mal. Il nous semble en tout cas que, dans le cas extrêmement répandu où le transformateur est à circuit magnétique unique, l’application de telles règles apparaît comme une solution palliative, peu satisfaisante, qu’il serait préférable d’abandonner au profit de l’approche consistant à réaliser les essais homopolaires.