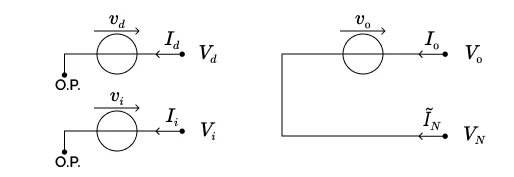
Si l’on ne souhaite pas sortir le neutre, alors on passe à un composant à 3 ports caractérisé par 7 variables (6 variables de ports et le potentiel du point neutre, qui devient une variable interne) et 4 équations :

\begin{equation}
\begin{cases}
V_d = v_d \\
V_i = v_i \\
V_0 – V_N = v_0 \\
I_0 = 0,
\end{cases}
\end{equation}

où l’on peut supprimer la variable interne qui n’apparaît que dans une seule équation $V_0 – V_N = v_0$ (en supprimant simultanément l’équation en question) pour aboutir simplement à :

\begin{equation} \label{eq:modele-symetrique-source-etoile} \begin{cases} V_d = v_d \\ V_i = v_i \\ I_0 = 0. \end{cases} \end{equation}

Remarque : Tout comme les charges à courant constant, cf la Remarque 26, le modèle (\ref{eq:modele-symetrique-source-etoile}) de la source de tension idéale est toujours découplé, quelle que soit la valeur de la tension imposée $v$. En ce sens, la source de tension idéale est toujours symétrique, même lorsque les tensions que l’on impose ne forment pas un système triphasé équilibré.

4.7.2 Source de tension en triangle idéale

4.7.2.1 Mise en équations en coordonnées usuelles

Les équations de la source de tension triangle idéale sont :

\begin{equation} \begin{cases} (I_3 – S) \, V_{ABC} = w \\ I_A + I_B + I_C = 0, \end{cases} \end{equation}

où $w$ est le vecteur constant des trois tensions composées imposées par la source. Le vecteur $w$ vérifie nécessairement la condition de compatibilité $\un^\top w = 0$, faute de quoi les trois premières équations sont incompatibles et le système linéaire complet dans lequel on les utilisera n’a pas de solution.

Remarque : Supposons la condition de compatibilité satisfaite, et supposons que ce composant soit intégré dans un réseau complet, non-pathologique, qui admet une solution unique. Serait-il habile d’utiliser les équations ci-dessus dans un solveur numérique pour essayer de la trouver ? Non : les trois premières équations sont en effet redondantes, ce qui mettra en échec la méthode de Newton qui sera certainement utilisée dans le solveur. Cette formulation, maladroite du point de vue numérique, est néanmoins celle que nous allons retenir pour nos calculs théoriques, pour conserver un jeu de trois équations invariant par permutation circulaire des variables ; nous supprimerons l’équation redondante plus tard, après le passage en coordonnées symétriques.

A ce stade, nous avons donc, de façon un peu inhabituelle, un composant à 6 variables et de 4 équations liées qui ne suppriment que 3 (et non pas 4) degrés de libertés. Ce composant dispose donc bien de 3 degrés de liberté comme il convient pour un composant à 3 ports.

4.7.2.2 Changement de base

Effectuons le changement de base sur les variables et sur les équations :

\begin{equation} \begin{cases} F^{-1} \, (I_3 – S) \, F \, V_{0id} = w_{0id} \\ I_0 = 0, \end{cases} \end{equation}

où $w_{0id} := F^{-1} w$, soit

\begin{equation} \begin{cases} w_0 = 0 \\ (1-a) V_i = w_i \\ (1-a^2) V_d = w_d \\ I_0 = 0. \end{cases} \end{equation}

La condition de compatibilité réapparaît dans la première équation, qui ne fait plus intervenir aucune variable et exige simplement la nullité de $w_0$, c’est-à-dire la satisfaction de l’équation $\un^\top w = 0$ que nous avions déjà bien en tête. En supprimant cette équation pour revenir à une formulation plus usuelle, et plus susceptible d’être utilisée pour le calcul numérique, à 3 équations non-liées, on obtient pour la source de tension triangle idéale :

\begin{equation} \begin{cases} V_d = \frac{1-a}{3} w_d \\ V_i = \frac{1-a^2}{3} w_i \\ I_0 = 0, \end{cases} \end{equation}

qui revient comme dans (\ref{eq:modele-symetrique-source-etoile}) à fixer les tensions directe et inverse à la valeur de son choix, et à annuler le courant homopolaire ; autrement dit, une source de tension en triangle est équivalente à une source de tension en étoile à neutre non-relié.

Remarque : Tout comme la source de tension en étoile, et les charges à courant complexe constant, la source de tension idéale en triangle est automatiquement symétrique : elle présente toujours les symétries décrites dans le chapitre 3, même lorsque les tensions que l’on impose ne forment pas un système triphasé équilibré. Pour être tout à fait explicite : une charge à courant constant quelconque, même si elle soutire à la fois du courant direct, du courant inverse et du courant homopolaire, doit être considérée comme un composant symétrique, bien que ceci ne soit guère conforme à l’idée que l’on se fait intuitivement d’un objet « symétrique ».

Schéma électrique symétrique

Le schéma électrique est le même que pour la source en étoile (en adaptant les valeurs des tensions directe et inverse).

4.7.3 Source de tension non-idéale

Une source de tension non-idéale est généralement modélisée par une source de tension idéale suivie d’une ligne symétrique simple à trois (section 4.2.1) ou à quatre (section 4.2.2) conducteurs.

4.7.4 Alternateur

Un alternateur, en régime permanent, est généralement modélisé par une source de tension en étoile suivie d’une ligne simple, à ceci près que les mutuelles directe et inverse $M_d$ et $M_i$ de cette « ligne simple équivalente » sont de valeurs très différentes (alors qu’elles sont égales pour une véritable ligne) : $M_d >> M_i$.

4.7.5 Sources de courant

Le cas des sources à courant complexe constant est identique à celui des charges à courant complexe constant, qui a été traité dans les parties 4.1.3 et 4.1.4.

4.7.6 Terre et mises à la terre

Nous considérons la terre comme un composant, au même titre que n’importe quel autre, et on peut envisager différents modèles pour la représenter.

La tradition électrotechnique est de la modéliser comme un conducteur parfait, autrement dit, comme un simple nœud, auquel on accède en passant par des impédances de mise à la terre (généralement non-nulles). On peut néanmoins tout à fait envisager de la représenter autrement.

Tout cela n’a presque pas d’importance dans le cadre de nos réflexions sur la théorie des composantes symétriques : la terre, quelle que soit la modélisation retenue, est en effet un composant qui ne possède aucun port triphasé, ce qui signifie que toutes ses variables (s’il y en a) seront isolées ; et aucun bloc triphasé d’équation, ce qui signifie que toutes ses équations (s’il y en a) seront isolées. Il n’y a donc aucun changement de base à prévoir : le modèle de la terre en composantes symétriques sera exactement le même qu’en composantes usuelles, au changement de variable $I_N \longrightarrow \tilde{I}_N$ près. Par exemple, dans un modèle où la terre est modélisée comme un simple nœud et où les mises à la terre sont représentées par des impédances (non-nulles) placées entre ce nœud de terre d’une part, et le point neutre de la charge équilibrée formée par les éléments transverses de la ligne d’autre part, le modèle formulé en variables usuelles comportera une équation du type
$$ V_\textrm{Terre} – V_N^\textrm{transverses} = Z_\textrm{MALT} \times I_N^\textrm{transverses}, $$
tandis que le modèle formulé en composantes symétriques comportera l’équation
$$ V_\textrm{Terre} – V_N^\textrm{transverses} = 3 \, Z_\textrm{MALT} \times \tilde{I}_N^\textrm{transverses}. $$
En d’autres termes, les impédances de mise à la terre seront multipliées par 3 dans le modèle en composantes symétriques par rapport à leur valeur réelle. Nous avions observé le même phénomène lorsque nous modélisions les lignes dans la partie 4.2 : les impédances (impédance propre et impédance mutuelle) du conducteur de neutre, de la même manière, étaient triplées dans le schéma électrique symétrique par rapport au schéma usuel.

Remarque : Si, selon l’habitude bien établie, on modélise la terre comme un simple nœud et qu’on en fait l’origine des potentiels, alors il n’est pas nécessaire de trop s’interroger sur la valeur des courants qui entrent dans ce nœud : puisque la terre porte le composant spécial, on n’y appliquera de toute façon pas la loi des nœuds.

Remarque : Notre présentation de la théorie des composantes symétriques fait apparaître le sujet de la modélisation de la terre comme relativement trivial. Il faut pourtant y faire un peu attention quand on lit la littérature tierce sur les composantes symétriques. En effet, de nombreux auteurs incluent les mises à la terre dans le modèle du composant couplé à la terre lui-même, contrairement à ce que nous proposons dans ce document.

Considérons par exemple un transformateur triangle-étoile dont le point neutre au secondaire est mis à la terre avec une certaine impédance. Cette impédance peut représenter un objet électrotechnique, par exemple une bobine, que l’on a délibérément ajoutée pour limiter les courants de court-circuit à la terre, comme on le fait parfois sur les transformateurs HT/MT ; ou alors l’impédance « naturelle » de la mise à la terre ; ou encore la somme des deux. Dans un modèle numérique, réalisé par exemple dans Roseau Load Flow, il nous semble plus clair, si ces deux phénomènes sont modélisés simultanément, d’utiliser explicitement deux impédances successives pour pouvoir les distinguer sans ambiguïté ; mais l’habitude des électrotechniciens semble plutôt être d’agréger les deux phénomènes dans une impédance unique. Pour l’analyse théorique, par opposition au calcul numérique, ceci est sans doute justifié : les équations seront plus compactes. Lorsqu’on utilise un logiciel de calcul comme Roseau Load Flow, en revanche, il semble préférable de désagréger les deux impédances pour pouvoir distinguer leurs effets respectifs.

Dans un tel cas, notre approche est de considérer le transformateur comme un composant ; l’impédance de mise à la terre comme un autre, voire comme deux autres (d’une part une partie délibérée, par exemple résistance de mise à la terre ou une bobine de Petersen, et d’autre part une partie subie liée à la nature du sol) ; et de relier ces composants entre eux via leurs ports.

Dans la littérature, au contraire, l’impédance de mise à la terre est souvent incluse directement dans le modèle du transformateur.

Jusque-là, la chose apparaît plutôt comme un détail dans le choix du périmètre des composants qu’on modélise, et ne semble pas avoir grande importance : on peut simplement objecter qu’inclure dans le modèle d’un composant appelé « transformateur » une impédance qui est due, au moins en partie, à la conduction dans la terre, est un peu trompeur.

Mais il y a pire : supposant implicitement que cette impédance sera attachée au traditionnel nœud de terre supraconducteur, certains auteurs tiennent directement compte de la (supposée) nullité du potentiel à l’extrémité de la mise à la terre dans les équations du transformateur, ce qui revient à mélanger une question de modélisation (du transformateur) avec une question de convention (le choix de l’origine des potentiels). Cette pratique, outre la confusion qu’elle engendre, empêche l’utilisation d’un tel modèle dans un réseau où la terre est modélisée de façon un peu plus subtile que par un supraconducteur (de potentiel nul), par exemple par un réseau d’impédances. Ce type de modèle de terre, cependant a-t-il un intérêt ? Est-il utilisé par quelqu’un ?