4.8 Défauts

Les défauts peuvent être vus comme des composants passifs presque comme les autres. Ils ont l’originalité d’être parfois connectés à la terre, certes, mais ceci se produit aussi dans le cas des lignes avec des éléments transverses et n’est donc pas une spécificité des défauts. En fait, la principale nouveauté qui va apparaître dans cette partie est que les défauts, contrairement à tous les composants que nous avons étudiés jusqu’à présent, ne sont généralement pas invariants par permutation circulaire des phases. Ceci n’empêche nullement de les modéliser en composantes symétriques ; simplement, il ne faudra pas espérer voir apparaître la structure circulante dans la matrice du composant, ni le découplage en trois sous-systèmes indépendants que cette structure engendre. Remarque 70: Comme nous l’avons déjà fait observer à la Remarque 25, ceci signifie qu’il ne sera pas utile dans cette partie d’effectuer le changement d’équations décrit dans la partie 3.3.2 : on se bornera à effectuer le passage en coordonnées symétriques, c’est-à-dire le changement de variables décrit dans la partie 3.3.1

4.8.1 Défaut triphasé franc

Commençons avec l’exception à la règle : le défaut triphasé franc, qui est bien un composant équilibré. Il peut être vu comme une charge triangle équilibrée d’impédance nulle. Ses équations symétriques et son schéma symétrique se déduisent donc de ceux de la charge triangle équilibrée, en prenant $Z=0$, soit : $$ V_d = 0, \quad V_i = 0, \quad I_0 = 0. $$ Le schéma électrique symétrique correspondant est présenté sur la Figure ci-dessous : 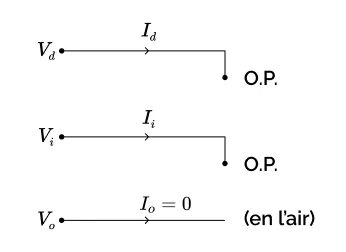Figure 4.41 : Schéma électrique symétrique du défaut triphasé franc

4.8.2 Défaut biphasé franc

Considérons maintenant un défaut biphasé franc entre les phases B et C.

Mise en équations en coordonnées usuelles

Les équations en coordonnées usuelles sont les suivantes : \begin{equation} \begin{cases} V_B = V_C \\ I_B + I_C = 0 \\ I_A = 0. \end{cases} \end{equation} En comptant $V_A$, qui fait partie des variables attachées au composant bien qu’elle n’intervienne pas dans les équations, le système comporte 6 variables qui sont toutes des variables de ports et qui forment 2 triplets triphasés. Il comporte par ailleurs 3 équations indépendantes, soit 3 degrés de liberté comme on s’y attend pour un composant à 3 ports.

Changement de base sur les triplets de variables triphasées

On commence par une petite astuce : $I_A$ étant nulle, on peut écrire la deuxième équation sous la forme $$ I_A + I_B + I_C = 0$$ qui permet de faire apparaître directement (trois fois) le courant homopolaire. On effectue ensuite le changement de base sur les deux triplets de variables triphasées : \begin{equation} \begin{cases} V_0 + a V_i + a^2 V_d = V_0 + a^2 V_i + a V_d \\ I_0 = 0 \\ I_0 + I_i + I_d = 0, \end{cases} \end{equation} soit \begin{equation} \begin{cases} V_i = V_d \\ I_i + I_d = 0 \\ I_0 = 0, \end{cases} \end{equation} que l’on peut interpréter comme un court-circuit entre les ports direct et inverse, le port homopolaire restant en l’air. On s’arrête là : il n’y a pas de bloc triphasé d’équation, et donc pas de notion de changement de base sur les blocs triphasés d’équations. Remarque 71: Le choix d’effectuer le court-circuit entre les phases B et C n’est pas anodin : si on l’effectuait entre A et B par exemple, alors les équations et leur interprétation ultérieure sous forme de schéma électrique seraient moins agréables.

Schéma électrique symétrique

Les équations symétriques du défaut biphasé-terre peuvent être interprétées comme celle du schéma électrique présenté ci-dessous : 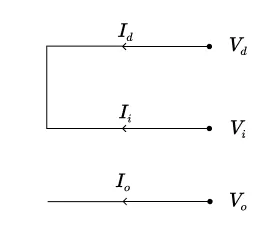Figure 4.42 : Schéma symétrique du défaut biphasé franc Remarque 72 : Ce schéma symétrique n’est pas constitué de trois schémas indépendants : le défaut étudié n’étant pas invariant par permutation circulaire des phases, il ne possède pas la propriété de découplage.

4.8.3 Défaut biphasé-terre

Considérons maintenant un défaut biphasé franc que nous allons épicer un peu en lui ajoutant un contact impédant avec la terre (ou le neutre). Ce cas se ramène à celui du pur défaut biphasé franc en faisant tendre vers l’infini l’impédance du contact avec la terre. Le défaut est placé entre B et C, cf la Remarque 71.

Mise en équations en coordonnées usuelles

Les équations en coordonnées usuelles sont les suivantes : \begin{equation} \label{eq:defaut-biphase-terre-usuel} \begin{cases} V_B = V_C \\ V_g – V_B = z \, I_g \\ I_B + I_C + I_g = 0 \\ I_A = 0. \end{cases} \end{equation} En comptant $V_C$ qui fait partie des variables attachées au composant bien qu’elle n’intervienne pas dans les équations, le système comporte 8 variables qui sont toutes des variables de ports et qui forment 2 triplets triphasés et 2 variables isolées. Il comporte par ailleurs 4 équations indépendantes, soit 4 degrés de liberté comme on s’y attend pour un composant à 4 ports.

Changement de base sur les triplets de variables triphasées

On commence par une petite astuce : $I_A$ étant nulle, on peut écrire la troisième équation sous la forme $$ I_A + I_B + I_C + I_g = 0 $$ qui permet de faire apparaître directement (trois fois) le courant homopolaire. On effectue ensuite le changement de base sur les deux triplets de variables triphasées : \begin{equation} \begin{cases} V_i = V_d \\ V_g – V_0 – a V_i – a^2 V_d = z \, I_g \\ 3 I_0 + I_g = 0 \\ I_0 + I_i + I_d = 0. \end{cases} \end{equation} On effectue ensuite le changement de variable $I_g \longrightarrow \tilde{I}_g := \frac{I_g}{3}$, et on simplifie un peu les autres équations au passage, pour obtenir : \begin{equation} \label{eq:defaut-biphase-terre-symetrique} \begin{cases} V_i = V_d \\ V_g – V_0 + V_d = 3 z \, \tilde{I}_g \\ \tilde{I}_g = I_0 \\ I_0 + I_i + I_d = 0. \end{cases} \end{equation} On s’arrête là : il n’y a pas de bloc triphasé d’équations, et donc pas de notion de changement de base sur les blocs triphasés d’équations.

Schéma électrique symétrique

Le schéma symétrique est présenté ci-dessous. 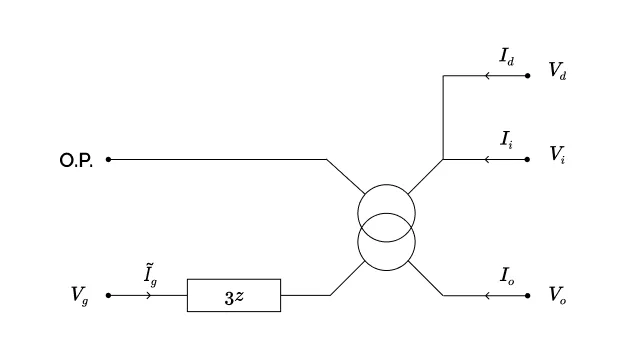Figure 4.43 : Schéma symétrique du défaut biphasé-terre Remarque : Le transformateur représenté sur la Figure 4.43 est un transformateur monophasé idéal de rapport 1, dont les enroulements sont orientés dans le sens usuel. Dans ces conditions, afin d’alléger le schéma, on n’y indique pas le rapport de transformation ni le sens des enroulements. Remarque : Dans le cas des charges équilibrées, le passage des équations symétriques au schéma symétriques était assez évident pour chacun des cas que nous avons étudié. Dans le cas des défauts, en revanche, on voit que cela commence à nécessiter un peu d’astuce. Remarque : Comme pour le défaut biphasé franc, on observe que le schéma symétrique obtenu n’est pas découplé en trois circuits indépendants.

4.8.4 Défaut monophasé impédant

On va maintenant traiter le cas du défaut monophasé, également appelé défaut phase-terre ou encore défaut homopolaire, qui consiste en un contact d’impédance $z$ entre la phase A et la terre, les phases B et C restant en l’air.

Mise en équations en coordonnées usuelles

L’équation du défaut est : \begin{equation} \begin{cases} I_B = 0,\\ I_C = 0,\\ V_g – V_A = z \, I_g\\ I_A + I_g = 0. \end{cases} \end{equation} Le système comporte 8 variables (dont $V_2$ et $V_3$ qui n’interviennent pas dans les équations) réparties en deux triplets triphasés et deux variables isolées. Il comporte par ailleurs 4 équations indépendantes, soit 4 degrés de liberté comme on s’y attend pour un composant à 4 ports.

Changement de variables

Effectuons le changement de variables : \begin{equation} \begin{cases} I_0 + a \, I_i + a^2 \, I_d = 0,\\ I_0 + a^2 \, I_i + a \, I_d = 0,\\ V_g – V_0 – V_i – V_d = z \, I_g\\ 3 \, I_0 + I_g = 0 \end{cases} \end{equation} où, comme dans le cas du défaut biphasé à la terre, nous avons de nouveau utilisé l’astuce qui consiste à remplacer le courant vers la terre $I_A$ par $3 I_0$ en exploitant le fait que $I_A = I_A + I_B + I_C$. On a alors une illumination en voyant les deux premières équations : puisque $1 + a + a^2 = 0$, leur solution évidente est la droite de coefficient directeur $(1, 1, 1)$ ; autrement dit, ces deux équations sont équivalentes à $I_i = I_d = I_0$. On effectue par ailleurs le changement de variable $I_g\longrightarrow \tilde{I}_g$ et on obtient : \begin{equation} \label{eq:defaut-monophase-equations-symetriques} \begin{cases} I_d = I_0\\ I_i = I_0\\ V_g – V_0 – V_i – V_d = 3 \, z \, \tilde{I}_g\\ I_0 + \tilde{I}_g = 0. \end{cases} \end{equation} On s’arrête là : il n’y a pas de bloc triphasé d’équations, donc pas de deuxième changement de base à effectuer.

Schéma électrique symétrique

Le schéma symétrique est présenté ci-dessous: 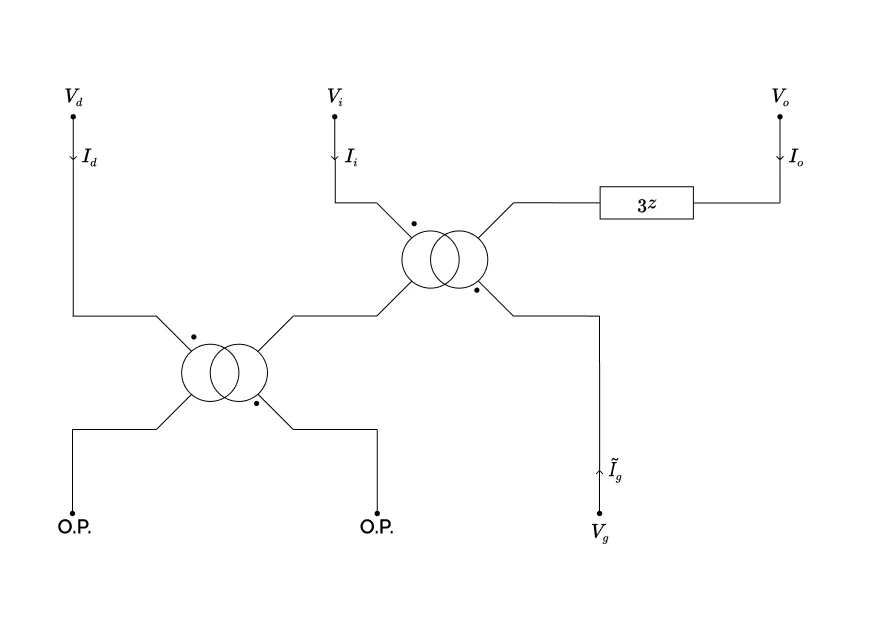Figure 4.44 : Schéma symétrique du défaut monophasé