Dans la section 4.1.5, nous avons vu comment réaliser l’effet de court-circuit homopolaire-neutre spécifique aux dispositifs « équilibreurs » en utilisant trois transformateurs monophasés couplés, les trois bobinages primaires auquel le réseau est raccordé étant couplés en étoile tandis que les trois bobinages secondaires n’étaient raccordés qu’entre eux, en triangle.
Dans cette configuration, la seule fonction du bobinage secondaire en triangle est d’imposer la nullité de la somme des tensions aux bornes des trois bobinages (secondaires, donc) primaires. Les bobinages primaires étant couplés en étoile, ceci revient à imposer
$$ (V_A – V_N) + (V_B – V_N) + (V_C – V_N) = 0 \Leftrightarrow V_N = \frac{V_A + V_B + V_C}{3}, $$
autrement dit à imposer l’égalité entre $V_N$ et $V_0$, autrement dit encore à réaliser l’effet de court-circuit homopolaire-neutre.
Or, les trois bobinages secondaires ayant le même nombre de spires et la tension étant proportionnelle au flux multiplié par le nombre de spires, imposer la nullité de la somme des trois tensions aux bornes des bobinages primaires revient à imposer la nullité de la somme des trois flux magnétiques dans les trois colonnes autour desquelles s’enroulent ces bobinages.
Dans la configuration de la section 4.1.5, où l’on utilisait trois transformateurs monophasés séparés, il était effectivement nécessaire d’ajouter le bobinage secondaire en triangle pour obtenir ce résultat : en effet, les trois circuits magnétiques étant indépendants, la valeur de chacun des trois flux pouvait a priori être absolument quelconque. En revanche, si l’on utilisait un circuit magnétique unique à trois colonnes, la nullité de la somme des trois flux serait garantie par construction, ce qui permettrait d’économiser le bobinage secondaire.
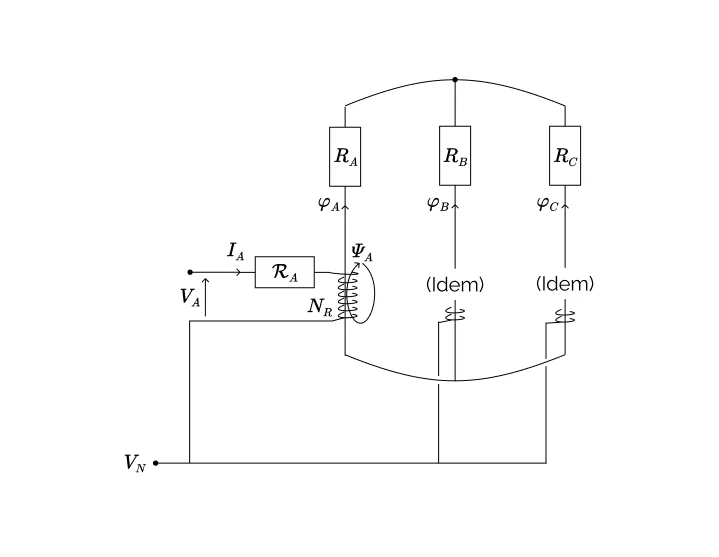
C’est cette configuration, représentée sur la figure suivante, que nous allons étudier dans cette partie.
Remarque 44
Un dispositif triphasé utilisant un circuit magnétique (c’est-à-dire souvent un transformateur, mais éventuellement une charge couplée comme dans le cas qui nous intéresse ici) est dit « à flux libre » s’il est constitué de trois circuits magnétiques séparés (c’est-à-dire, dans le cas d’un transformateur triphasé, de trois transformateurs monophasés) ou s’il possède un circuit magnétique unique à 4 ou 5 colonnes. Dans ce cas, les trois flux dans les trois colonnes peuvent prendre n’importe quelle valeur, et peuvent notamment être (non-nuls et) égaux entre eux ; c’est ce qui se produit quand on fait circuler dans les bobinages un courant purement homopolaire.
Inversement, le dispositif est dit « à flux forcé » lorsqu’il est constitué d’un circuit magnétique unique à trois colonnes ; dans ce cas, la somme des trois flux magnétiques dans les trois colonnes du transformateur est nécessairement nulle. C’est cette caractéristique que nous cherchons à exploiter ici.
Modélisation
Tous les circuits que nous avons étudiés jusqu’à présent étaient constitués par l’assemblage de composants que nous savions déjà modéliser:
- de simples impédances, d’une part,
- et d’autre part des transformateurs monophasés (non-idéaux) pour lesquels nous avons eu recours au modèle classique qui est présenté dans le Chapitre 2.
Nous faisons maintenant face à un composant nouveau, impliquant un circuit magnétique commun, et pour lequel nous ne disposons pas encore d’un modèle électrique. Nous allons donc devoir modéliser notre composant en partant de son circuit magnétique, puis nous éliminerons les variables et les paramètres magnétiques pour revenir à un modèle purement électrique.
Sur la figure précédente, on a noté $\R$ la réluctance de chacune des trois colonnes supposées identiques du circuit magnétique. On introduit également son inverse :
$$ \Y := \frac{1}{\R}, $$
ainsi que la longueur $l$ et la section $S$ de chacune de nos trois colonnes identiques.
Ces trois réluctances sont traversées par les flux $\phi_A$, $\phi_B$ et $\phi_C$ respectivement.
Le nombre de spires de chacun des trois bobinages, supposés identiques, est noté $N$.
La résistance d’un bobinage est notée $R$.
Dans chaque bobinage, on considère également l’existence d’un flux de fuite, dont les lignes de champ échappent au circuit magnétique et dont les flux associés sont notés $\phi^f_A$, $\phi^f_B$ et $\phi^f_C$. Ces flux sont supposés traverser une certaine réluctance de fuite que l’on ne sait pas bien estimer a priori (c’est-à-dire avant d’avoir construit l’objet étudié) et dont la valeur ne pourra probablement être déterminée qu’a posteriori (c’est-à-dire en faisant des essais sur l’objet physique une fois que nous l’aurons construit).
Cette réluctance de fuite, supposée identique pour chacun des trois bobinages, est notée $\R^f$ et son inverse est notée $\Y^f$.
Enfin, on suppose l’existence de pertes fer qui ne sont pas représentées sur la figure à ce stade ; nous les introduirons ultérieurement.
Les équations de notre système, en l’absence pour le moment des pertes fer, sont les suivantes.
\begin{equation}
\begin{cases}
V_A – V_N = R \, I_A + N \frac{d\phi_A}{dt} + N \frac{d\phi^f_A}{dt} = R \, I_A + j \omega N \phi_A + j \omega N \phi^f_A \\
V_B – V_N = R \, I_B + N \frac{d\phi_B}{dt} + N \frac{d\phi^f_B}{dt} = R \, I_B + j \omega N \phi_B + j \omega N \phi^f_B \\
V_C – V_N = R \, I_C + N \frac{d\phi_C}{dt} + N \frac{d\phi^f_C}{dt} = R \, I_C + j \omega N \phi_C + j \omega N \phi^f_C\\
I_A + I_B + I_C + I_N = 0\\
N \, I_A – \R^f \, \phi^f_A = 0\\
N \, I_B – \R^f \, \phi^f_B = 0\\
N \, I_C – \R^f \, \phi^f_C = 0\\
N \, I_A – \R \, \phi_A = \alpha\\
N \, I_B – \R \, \phi_B = \alpha\\
N \, I_C – \R \, \phi_C = \alpha\\
\phi_A + \phi_B + \phi_C = 0,
\end{cases}
\end{equation}
où $\alpha$ est la chute de force magnéto-motrice (identique) sur chacune des trois colonnes.
Ce système compte 15 variables (8 variables de ports, électriques, et 7 variables internes, magnétiques) et 11 équations~; soit 4 degrés de liberté, comme on s’y attend pour un composant à 4 ports.
Les quatre dernières équations sont équivalentes à
\begin{equation}
\begin{cases}
\phi_A = \Y (N \, I_A – \alpha)\\
\phi_B = \Y (N \, I_B – \alpha)\\
\phi_C = \Y (N \, I_C – \alpha)\\
\alpha = \frac{N I_A + N I_B + N I_C}{3},
\end{cases}
\end{equation}
ce qui permet d’éliminer $\alpha$ via la dernière équation :
\begin{equation}
\begin{cases}
\phi_A = \Y \big(\frac{2}{3} N I_A – \frac{1}{3} N I_B – \frac{1}{3} N I_C \big) \\
\phi_B = \Y \big(\frac{2}{3} N I_B – \frac{1}{3} N I_C – \frac{1}{3} N I_A \big) \\
\phi_C = \Y \big(\frac{2}{3} N I_C – \frac{1}{3} N I_A – \frac{1}{3} N_B I_B \big)
\end{cases}
\end{equation}
On peut ensuite d’éliminer $\phi_A$, $\phi_B$ et $\phi_C$ par substitution dans les équations restantes. Celles-ci deviennent :
\begin{equation}
\begin{cases}
V_A – V_N = (R + j \omega (N^2 \Y^f + \frac{2 N^2 \Y}{3})) I_A – j \omega (\frac{N^2 \Y}{3}) I_B – j \omega (\frac{N^2 \Y}{3}) I_C \\
V_B – V_N = (R + j \omega (N^2 \Y^f + \frac{2 N^2 \Y}{3})) I_B – j \omega (\frac{N^2 \Y}{3}) I_C – j \omega (\frac{N^2 \Y}{3}) I_A \\
V_C – V_N = (R + j \omega (N^2 \Y^f + \frac{2 N^2 \Y}{3})) I_C – j \omega (\frac{N^2 \Y}{3}) I_A – j \omega (\frac{N^2 \Y}{3}) I_B \\
I_A + I_B + I_C + I_N = 0.
\end{cases}
\end{equation}
En introduisant les inductances
\begin{equation}
\label{eq:equilibreur-etoile-L}
L := \frac{2}{3} N^2 \Y,
\end{equation}
\begin{equation}
\label{eq:equilibreur-etoile-M}
M := \frac{1}{3} N^2 \Y,
\end{equation}
et
\begin{equation}
L^f := N^2 \Y^f,
\end{equation}
le système devient
\begin{equation}
\begin{cases}
V_A – V_N = (R + j \omega (L^f + L)) I_A – j \omega M I_B – j \omega M I_C \\
V_B – V_N = (R + j \omega (L^f + L)) I_B – j \omega M I_C – j \omega M I_A \\
V_C – V_N = (R + j \omega (L^f + L)) I_C – j \omega M I_A – j \omega M I_B \\
I_A + I_B + I_C + I_N = 0.
\end{cases}
\end{equation}
Ces équations sont celles du circuit électrique représenté sur la figure suivante, sur laquelle on a également ajouté en traits pointillés trois résistances supplémentaires notées $R_f$. Ces trois résistances supplémentaires modélisent les pertes fer ; cette manière de les représenter se justifie par les mêmes arguments que pour le transformateur monophasé non-idéal qui est présenté dans le Chapitre 2.
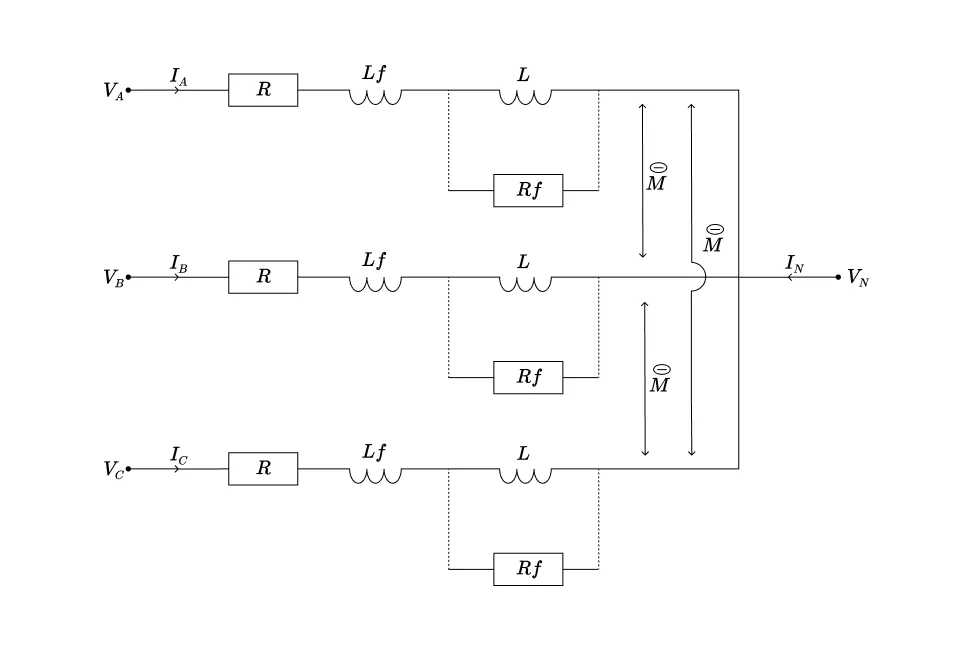
Ainsi, pour la colonne A par exemple, la tension aux bornes de l’inductance $L$ est égale à
$$ U^L_A := N \frac{d\phi_A}{dt} = N S \frac{dB_A}{dt} = j N S \omega B_A, $$
de sorte que les pertes fer totales sur l’ensemble du volume $Sl$ de la colonne A sont égales à
$$ (S l) \alpha \frac{|U^L_A|^2}{(N S \omega)^2} = \frac{ \alpha l}{N^2 \omega^2 S} |U^L_A|^2. $$
Ces pertes sont identiques à celles que produirait une résistance de valeur
\begin{equation}
\label{eq:equilibreur-etoile-Rfer}
R_f := \frac{N^2 \omega^2 S}{\alpha l}
\end{equation}
soumise à la tension $U^L_A$ : c’est ce qui justifie l’introduction de la résistance $R_f$ en parallèle de l’inductance $L$ dans le schéma de la figure précédente.
Avec cette modification du modèle, les équations deviennent :
\begin{equation}
\label{eq:equilibreur-etoile-final}
\begin{cases}
V_A – V_N = (R + j \omega L^f + Z_f) I_A – j \omega M I_B – j \omega M I_C \\
V_B – V_N = (R + j \omega L^f + Z_f) I_B – j \omega M I_C – j \omega M I_A \\
V_C – V_N = (R + j \omega L^f + Z_f) I_C – j \omega M I_A – j \omega M I_B \\
I_A + I_B + I_C + I_N = 0
\end{cases}
\end{equation}
où
$$ Z_f := (j \omega L) // R_f = \frac{R_f \, (j \omega L)}{j \omega L + R_f}. $$
Remarque 45:
En introduction de cette section, nous avons annoncé notre intention d’éliminer les variables et les paramètres magnétiques pour obtenir un modèle purement électrique, ce à quoi nous sommes effectivement parvenus à l’équation (\ref{eq:equilibreur-etoile-final}). En ce qui concerne les variables magnétiques, cette opération d’élimination n’appelle pas de commentaire particulier : celles-ci étant des variables internes au composant, et non pas des variables de ports, on peut les éliminer selon son bon plaisir comme n’importe quelles variables internes. En ce qui concerne les paramètres magnétiques en revanche, l’opération d’élimination est un peu plus significative du point de vue physique. En effet, le fait de raisonner à partir de la physique du circuit magnétique permet de donner une valeur aux paramètres du modèle électrique qui représentent des phénomènes magnétiques ; plus précisément,
- les valeurs de l’inductance magnétisante $L$ et de l’inductance mutuelle $M$ peuvent être évaluées grâce aux équations (\ref{eq:equilibreur-etoile-L}) et (\ref{eq:equilibreur-etoile-M}),
- et la valeur de la résistance $R_f$ qui modélise les pertes fer peut de même être évaluée à partir de l’équation (\ref{eq:equilibreur-etoile-Rfer}).
Cependant, lorsque l’on considère le modèle électrique de la Figure précédente, on omet souvent de fournir les formules en question, et l’on considère plutôt que la bonne manière de déterminer les valeurs de l’inductance magnétisante $L$, de l’inductance mutuelle $M$ et de la résistance $R_f$ est de réaliser des essais (essai à vide, essai en court-circuit…), au mieux en vérifiant a posteriori que les valeurs trouvées ne sont pas trop éloignées des valeurs prédites par les équations (\ref{eq:equilibreur-etoile-L}), (\ref{eq:equilibreur-etoile-M}) et (\ref{eq:equilibreur-etoile-Rfer}). C’est aussi en ce sens que l’on peut parler d’élimination des paramètres magnétiques : on oublie délibérément en quoi ces paramètres déterminent certains paramètres du modèle électrique.
Cette approche présente évidemment l’inconvénient majeur de nécessiter l’existence matérielle du composant : on ne peut caractériser le modèle par des essais qu’après avoir construit l’objet, ce qui n’est guère adapté lorsqu’on parle d’un composant hypothétique, par exemple lorsqu’on est en phase ce conception. De plus, réaliser des essais est généralement assez laborieux, plus difficile en tout cas qu’appliquer une formule mathématique toute simple. Cependant, le fait de passer par des essais présente aussi des avantages considérables :
- cela permet de valider le modèle, du moins si l’on prend la peine de réaliser suffisamment d’essais (et non pas le strict minimum, c’est à dire autant d’essais que de paramètres à ajuster) : on verra alors en effet à quel point l’objet physique ressemble ou non à son idéal mathématique ;
- les valeurs des paramètres obtenues par mesure directe sont certainement plus fiables que celles qui sont obtenues de façon indirecte par l’intermédiaire d’un travail de modélisation ;
- la méthode des essais permet de caractériser aussi l’inductance de fuite, sur laquelle notre approche théorique est muette : nous avons simplement considéré qu’il existait des fuites de flux et qu’à ceux-ci s’opposait une certaine réluctance $\R^f$ que notre théorie ne nous permet pas de calculer.
De la même manière, d’ailleurs, la résistance des bobinages (qui est cette fois un paramètre électrique et non pas magnétique) est généralement déterminée par des essais lorsque l’objet existe, et peut aussi être estimée en partant des caractéristiques du conducteur (résistivité du matériau, section, longueur) lorsque l’on est en phase de conception.
Structure du système d’équations en coordonnées usuelles
On écrit le système d’équations par blocs :
\begin{equation}
\label{eq:equilibreur-etoile-modele-elec-complet}
\begin{cases}
V_{ABC} – V_N \un = N \, I_{ABC} \\
\un^\top I_{ABC} + I_N = 0
\end{cases}
\end{equation}
où
\begin{equation}
N :=
\begin{bmatrix}
R + j \omega L^f + Z_f & – j \omega M & – j \omega M \\
– j \omega M & R + j \omega L^f + Z_f & – j \omega M \\
– j \omega M & – j \omega M & R + j \omega L^f + Z_f
\end{bmatrix}.
\end{equation}
Ce système possède la structure circulante. De plus, toutes les sous-matrices circulantes $3 \times 3$ vérifient $\beta = \gamma$ ; au vu de la Remarque 4, on s’attend donc à ce que les systèmes direct et inverse soient identiques.
Changement de base
On effectue le changement de base sur les variables et les équations du système (\ref{eq:equilibreur-etoile-modele-elec-complet}) :
\begin{equation}
\begin{cases}
V_{0id} – V_N \, F^{-1} \un = F^{-1} \, N \, F \, I_{0id} \\
\un^\top F \, I_{0id} + I_N = 0
\end{cases}
\end{equation}
soit, tous calculs faits et en introduisant le changement de variable $I_N \longrightarrow \tilde{I}_N$,
\begin{equation}
\begin{cases}
V_0 – V_N = (R + j \omega L^f + Z_f – 2 j \omega M) \, I_0 \\
V_i = (R + j \omega L^f + Z_f + j \omega M) \, I_i \\
V_d = (R + j \omega L^f + Z_f + j \omega M) \, I_d \\
I_0 + \tilde{I}_N = 0.
\end{cases}
\end{equation}
La résistance $R_f$ qui modélise les pertes fer est généralement élevée devant l’impédance magnétisante $j \omega L$, de sorte que
$$ Z_f := (j \omega L) // R_f \approx j \omega L, $$
et d’après (\ref{eq:equilibreur-etoile-L}) et (\ref{eq:equilibreur-etoile-M}), on a $L = 2 M$, soit
$$ R + j \omega L^f + Z_f – 2 j \omega M \approx R + j \omega L^f \approx 0~; $$
on retrouve donc bien l’effet de court-circuit homopolaire-neutre attendu d’un dispositif équilibreur.
Schéma électrique symétrique
Le circuit est comme d’habitude équivalent à trois impédances directe, inverse et homopolaire, les deux premières étant égales entre elles et données par
$$ R + j \omega L^f + Z_f + j \omega M $$
tandis que la dernière est donnée par
$$ R + j \omega L^f + Z_f – 2 j \omega M. $$