Ce chapitre expose de façon complètement abstraite, sans faire référence à tel ou tel composant particulier, comment la théorie des composantes symétriques permet de simplifier considérablement les équations d’un composant triphasé pourvu que celui-ci présente ce que nous appellerons la symétrique d’invariance par permutation circulaire des phases. Cette simplification des équations se manifestera de deux manières :
- D’une part, les équations symétriques d’un tel composant triphasé sont généralement très creuses, car les matrices qu’elles font intervenir sont toutes diagonales ;
- et d’autre part, ces équations se présentent sous la forme de trois systèmes d’équations découplés.
Dans le chapitre suivant, nous appliquerons ensuite cette approche générale à tous les composants triphasés usuels.
3.1 Variables
3.1.1 Variables triphasées et variables isolées
On considère un composant électrotechnique triphasé, c’est-à-dire auquel sont associés \(n\) triplets de variables complexes (Il s’agit généralement de variables de potentiel ou de courant, mais on pourrait aussi imaginer par exemple un triplet de flux magnétiques dans les trois colonnes d’un transformateur, si l’on souhaite expliciter ces flux magnétiques dans le modèle.).
Notre composant est supposé passif ; on exclut donc temporairement le cas des sources, qui sera traité à part dans la partie 4.7.
On note ces variables \(X^1_{ABC}\), \(X^2_{ABC}\)… l’indice \(ABC\) suggérant que la première variable du triplet est associée à la phase \(A\), le deuxième à la phase \(B\) et le troisième à la phase \(C\).
Remarque :
Cette notation est un peu abusive car, dans certains cas, cette association n’est pas évidente ; par exemple, dans le cas du triplet des courants dans un enroulement en triangle, chaque courant est plutôt associé à une paire de phase (et à une orientation au sein de cette paire). Dans ce cas de figure, il faut garder en tête que \(X_{ABC}\) représente par exemple :
- non pas « le courant associé à la phase A, respectivement B, respectivement C » ;
- mais plutôt : « le courant qui va de A vers B, respectivement de B vers C, respectivement de C vers A » (ou toute autre convention).
À ce composant peuvent également être associées d’autres variables qui ne constituent pas un triplet triphasé : courant entrant dans un point neutre, etc. On les appelle les variables isolées et on les regroupe dans un vecteur \(y\).
3.1.2 Variables internes et externes
Certaines variables triphasées seront externes, c’est-à-dire qu’elles constitueront les variables de port des ports triphasés de notre composant : pour tout composant triphasé, on aura ainsi toujours au minimum un triplet triphasé de variables de potentiel (« \(V_{ABC}\) ») et un triplet triphasé de variables de courant (« \(I_{ABC}\) ») ; et éventuellement plusieurs paires de tels triplets, si le composant possède plusieurs ports triphasés, comme dans le cas d’une ligne ou d’un transformateur.
D’autres variables triphasées peuvent être internes, comme le cas du triplet des courants dans un triangle.
De même, certaines variables isolées peuvent être externes, comme le courant qui entre dans un port de neutre (sorti), et d’autres internes, comme le potentiel d’un point neutre non-sorti.
3.2 Équations
3.2.1 Hypothèse d’invariance par permutation circulaire des phases
De nombreux composants triphasés sont invariants par permutation circulaire des phases : ils se comportent exactement de la même manière si l’on renomme leurs phases « B, C, A » ou « C, A, B » au lieu de « A, B, C ». Autrement dit, pour de nombreux composants, il est indifférent du point de vue physique d’effectuer une permutation circulaire des étiquettes qui identifient les trois phases sur le bornier de connexion du composant. C’est cette propriété que nous allons chercher à exploiter dans cette partie. Remarque : Dans cette opération, tous les triplets triphasés doivent être renommés simultanément : on renommera par exemple dans l’ordre \(B\), \(C\), \(A\) à la fois les variables de potentiel et de courant du port primaire d’un transformateur triangle-étoile, et les variables de potentiel et de courant de son port secondaire, et les courants dans l’enroulement triangle, qui forment un triplet triphasé de variables internes. Les variables associées au point neutre de l’étoile, qui n’appartiennent pas à un triplet triphasé, ne seraient en revanche pas affectées. Remarque : Pour les composants passifs que nous étudions dans cette partie, la définition ci-dessus de la propriété d’invariance par permutation circulaire des phases est assez intuitive, et ne pose pas de difficulté particulière. En revanche, elle est assez subtile dans le cas des sources, c’est-à-dire des composants à tension ou à courant constant. Nous reviendrons sur ce point.3.2.2 Blocs triphasés d’équations et équations isolées
À notre composant sont également associées des équations, linéaires par hypothèse dans cet ouvrage, dont certaines forment elles-mêmes naturellement des blocs de trois équations que nous appellerons également des blocs triphasés d’équations. Par exemple, si l’on modélise une charge en étoile, on va écrire trois équations similaires, chacune associée à l’une des branches de l’étoile ; ces trois équations formeront un bloc triphasé. Remarque : On associe souvent mentalement la première équation à la phase A, la deuxième à la phase B et la troisième à la phase C. Comme pour les variables, il faut garder en tête que cette association peut être trompeuse~; en effet, ces équations ne feront généralement pas uniquement intervenir des variables associées à la phase A, puisqu’il peut exister des couplages entre les phases. D’autres équations seront isolées, au sens où elles n’appartiendront pas à un bloc triphasé. Dans le modèle d’une charge sans point neutre ou à neutre non-sorti, par exemple, on trouvera certainement l’équation \(I_A + I_B + I_C = 0\), qui n’appartiendra pas à un bloc triphasé d’équations. En notant \(m\) le nombre de blocs triphasés, le système linéaire aura donc la forme suivante : \begin{equation} \label{eq:forme-generale-sys-lineaire} \begin{bmatrix} A_1^1 & \dots & A_1^n & A_1 \\ \vdots & & \vdots & A_2 \\ A_m^1 & \dots & A_m^n & A_m \\ A^1 & \dots & A^n & A \\ \end{bmatrix} \times \begin{bmatrix} X_{ABC}^1 \\ \vdots \\ X_{ABC}^n \\ y \end{bmatrix} = 0, \end{equation} où l’on a placé :- Dans le vecteur des variables, tous les triplets de variables triphasées (triplets de potentiels, de courants, de flux magnétiques\dots) en premier ; et en dernier, regroupées dans le vecteur \(y\), les variables isolées;
- et dans le système d’équations, les blocs triphasés d’équations en premier, et les équations isolées en dernier.
3.2.3 Matrices à structure circulante
Un bloc d’équation triphasé d’indice \(i \in \{1, \dots m\}\) dans la matrice ci-dessus est dit circulant lorsque :- chacun des blocs \(A_i^j\) (\(j \in \{1, \dots n\}\)) qui apparaît dans ce bloc est une matrice circulante,
- le bloc \(A_i\) vérifie \(S^\top A_i = A_i\) où \(S\) est la matrice de décalage définie plus haut dans ce document ; autrement dit, lorsque toutes les colonnes de \(A_i\) sont des multiples de \(\mathbf{1}\).
- tous ses blocs triphasés d’équations sont circulants,
- et \(\forall j \in \{1,\dots n\} : A^j S = A^j\) ; autrement dit, lorsque toutes les lignes de \(A^j\) sont des multiples de \(\mathbf{1}^\top\).
3.3 Diagonalisation
Supposons que notre composant soit modélisé par l’équation \eqref{eq:forme-generale-sys-lineaire} dans laquelle la matrice possède la structure circulante, et passons en coordonnées symétriques.3.3.1 Changement de base pour les variables triphasées
Au sens strict, passer en coordonnées symétriques consiste à changer de base les variables triphasées \(X^j_{ABC}\) (\(j \in \{1,\dots n\}\)). Le problème devient : \begin{equation} \begin{bmatrix} A_1^1 & \dots & A_1^n & A_1 \\ \vdots & & \vdots & \vdots \\ A_m^1 & \dots & A_m^n & A_m \\ A^1 & \dots & A^n & A \\ \end{bmatrix} \times \begin{bmatrix} F & 0 & \dots & 0 & 0 \\ 0 & F & \dots & 0 & 0 \\ \vdots & & & \vdots & 0 \\ 0 & 0 & \dots & F & 0 \\ 0 & 0 & \dots & 0 & I \end{bmatrix} \times \begin{bmatrix} X_{0id}^1 \\ \vdots \\ X_{0id}^n \\ y \end{bmatrix} = 0, \end{equation} où \(I\) représente la matrice identité de la dimension de \(y\). Remarque : Le changement de variables ne concerne que les triplets de variables triphasées, c’est-à-dire les \(X^j_{ABC}\) ; la variable \(y\) qui rassemble les variables isolées, elle, est inchangée. De façon équivalente, on peut écrire : \begin{equation} \begin{bmatrix} A_1^1 F & \dots & A_1^n F & A_1 \\ \vdots & & \vdots & \vdots \\ A_m^1 F & \dots & A_m^n F & A_m \\ A^1 F & \dots & A^n F & A \\ \end{bmatrix} \times \begin{bmatrix} X_{0id}^1 \\ \vdots \\ X_{0id}^n \\ y \end{bmatrix} = 0. \end{equation}3.3.2 Changement de base pour les blocs triphasés d’équations
Notre système est maintenant représenté en coordonnées symétriques, certes, mais nous n’allons pas nous arrêter là car nous n’avons toujours pas exploité la propriété de diagonalisation des matrices circulantes par la matrice de Fortescue ; et nous n’avons donc toujours pas fait apparaître la moindre matrice diagonale. Pour cela, une deuxième opération est nécessaire : appliquer également le changement de variables aux blocs triphasés d’équations, c’est-à-dire pré-multiplier tout notre système par la matrice inverse de celle que nous venons d’introduire. Par analogie avec la terminologie utilisée par les variables, les trois nouvelles équations de chaque bloc seront appelées « l’équation homopolaire », « l’équation inverse » et « l’équation directe ». Le système devient : \begin{equation} \begin{bmatrix} F^{-1} A_1^1 F & \dots & F^{-1} A_1^n F & F^{-1} A_1 \\ \vdots & & \vdots & \vdots \\ F^{-1} A_m^1 F & \dots & F^{-1} A_m^n F & F^{-1} A_m \\ A^1 F & \dots & A^n F & A \\ \end{bmatrix} \times \begin{bmatrix} X_{0id}^1 \\ \vdots \\ X_{0id}^n \\ y \end{bmatrix} = 0. \end{equation}3.3.3 Conséquences du double changement de base
Nous venons de faire apparaître \(nm\) blocs diagonaux de taille \(3 \times 3\) dans notre système. C’est ce qui rentabilise le changement de variables : si nous nous étions contentés de la première opération, c’est-à-dire si nous avions effectué le changement de base sur les variables triphasées seulement et pas sur les équations triphasées, alors nous serions certes passés en coordonnées symétriques ; mais la structure de nos équations ne s’en serait pas spécialement trouvée améliorée. Une dernière observation est que, au vu de la structure particulière des matrices \(A_i\) (dont les colonnes sont des multiples de \(\mathbf{1}\)) et des matrices \(A^j\) (dont les lignes sont des multiples de \(\mathbf{1}^\top\)),- les deux dernières colonnes des matrices \(A^j F\) seront nulles, ce qui signifie que les équations isolées ne feront intervenir que des variables isolées (terme \(y\)) et des variables homopolaires, à l’exclusion des variables directes et inverses.
- Les deux dernières lignes des matrices \(F^{-1} A_i\) seront nulles, ce qui signifie que les équations inverses et directes ne feront pas intervenir les variables isolées \(y\).
- on choisit d’effectuer le changement de variables (et d’équations) pour le réseau amont (symétrique par hypothèse) car cela en simplifie les équations ;
- on exprime les équations du défaut en coordonnées usuelles parce que c’est la manière la plus naturelle de procéder ;
- on se retrouve avec deux jeux d’équations écrits avec deux jeux de variables différents reliés par des équations de passage 6 ;
- et on préfère donc passer les équations du défaut en coordonnées symétriques, non pas parce que cela est avantageux du point de vue de la modélisation du défaut (ça ne l’est pas), mais pour que l’ensemble du problème soit décrit dans un seul et même jeu d’inconnues.
3.4 Interprétation électrique de la diagonalisation
3.4.1 Découplage du modèle d’un composant triphasé équilibré
Les variables inverses n’apparaissent que dans les équations inverses ; les variables directes, que dans les équations directes ; et les variables homopolaires et isolées, que dans les équations homopolaires et isolées.
L’aboutissement de notre changement de variables, sur les variables triphasées et sur les blocs triphasés d’équations, à partir d’une matrice qui possède la structure circulante, est donc un système linéaire (non seulement très creux mais aussi) découplé, dans lequel on peut regrouper entre elles :
- d’une part toutes les équations inverses, pour former un système linéaire indépendant qui ne porte que sur les variables inverses, et que l’on appellera le « modèle inverse » ;
- d’autre part, toutes les équations directes, pour former un système linéaire indépendant qui ne porte que sur les variables directes, et que l’on appellera le « modèle direct » ;
- et enfin, toutes les équations homopolaires et isolées, pour former un système linéaire indépendant qui ne porte que sur les variables homopolaires et isolées, et que l’on appellera simplement « le système homopolaire » pour faire court, mais dont il ne faudra pas oublier qu’il implique aussi les variables isolées.
Cette propriété de découplage signifie notamment que le schéma électrique équivalent au jeu d’équations sera en fait constitué de trois circuits indépendants. Un composant équilibré sera donc équivalent, en coordonnées symétriques, à trois composants distincts.
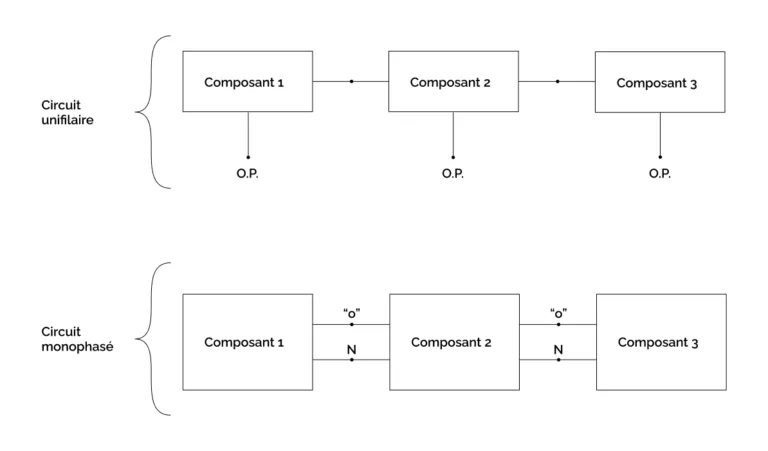
3.4.2 Modèles unifilaires et modèles monophasés
Le circuit inverse ne fera intervenir que des potentiels et des courants inverses, comme s’il constituait un circuit à un seul conducteur représentant uniquement la composante inverse de la phase A du circuit original. On désignera donc ce circuit comme « unifilaire ». De même, le circuit direct sera unifilaire.
En revanche, le circuit homopolaire fera intervenir à la fois les variables homopolaires et les variables isolées, notamment celles associés au conducteur de neutre quand il existe : dans ce cas, le circuit homopolaire sera « monophasé », par opposition à « unifilaire », c’est-à-dire composé de deux conducteurs.