Logo de Roseau Technologies - Solutions logicielles simples, modernes et ergonomiques pour la modélisation des réseaux de distribution d'électricité, à destination des GRD
Nous contacter
Composantes symétriques - Modélisation des transformateurs monophasés

Partie 2 – Modélisation des transformateurs monophasés

Coordonnées usuelles et coordonnées symétriques

Avant de revenir à l’étude des composants triphasés et de leurs symétries, nous allons consacrer ce chapitre à l’étude de plusieurs variantes de modèle de transformateur monophasé ; ceci nous permettra d’introduire différentes notions dont nous aurons besoin dans la suite de cet ouvrage lorsque nous étudierons les modèles symétriques de transformateurs triphasés. Il ne sera donc pas question dans ce chapitre de la théorie des composantes symétriques elle-même, mais nous préparerons le terrain pour son introduction dans les chapitres ultérieurs.

2.1 Transformateur idéal à rapport de transformation complexe

On considère un convertisseur monophasé dont on note \(V\) et \(I\) la tension et le courant au primaire, tandis que \(V’\) et \(I’\) représentent la tension et le courant au secondaire. On suppose que le convertisseur est modélisé par les équations

\begin{equation}
\begin{cases}
V = \mu \, V’ \\
I’ + \nu \, I = 0,
\end{cases} \quad
\mu, \nu \in \mathbb{C};
\end{equation}

qui sont similaires à celles d’un transformateur monophasé classique, à ceci près que les coefficients de transformation \(\mu\) et \(\nu\) sont complexes.

La puissance complexe qui entre dans le secondaire de notre composant est

\[V’ \, (I’)^* = \left(\frac{1}{\mu} \, V\right) \, (-\nu \, I)^* = – \left(\frac{\nu^*}{\mu}\right) V \, I^*.\]

Ainsi, notre composant conserve la puissance complexe si et seulement si les deux rapports de transformation, celui des tensions (\(\mu\)) et celui des courants (\(\nu\)), sont mutuellement conjugués, autrement dit si et seulement si \(\mu = \nu^*\).

Lorsque cette propriété est vérifiée, on qualifie ce composant de « transformateur complexe idéal ». Il caractérisé par les équations

\begin{equation}
\begin{cases}
V = \mu \, V’ \\
I’ + \mu^* \, I = 0,
\end{cases} \quad
\mu \in \mathbb{C}.
\end{equation}

Le paramètre \(\mu \in \mathbb{C}\) est appelé le rapport de transformation (complexe) du transformateur complexe idéal.

Remarque : Cette notion de « rapport de transformation », d’une part, n’indique pas de quel côté se trouvent le primaire et le secondaire ; et d’autre part singularise l’équation des tensions, où intervient effectivement le paramètre \(\mu\), par rapport à l’équation des courants, où ce n’est pas \(\mu\) lui-même mais son conjugué qui intervient.
Remarque : Le transformateur monophasé à rapport de transformation complexe n’existe pas, il s’agit d’un composant fictif. Son introduction est motivée par le fait que ce composant nous sera utile pour modéliser les transformateurs triphasés dans le cadre de la théorie des composantes symétriques.
Remarque : Le déphasage entre la tension primaire et la tension secondaire est donné par l’argument du nombre complexe \(\mu\) :
\[\arg(V’) – \arg(V) = -\arg(\mu).\]
Lorsque ce déphasage est un multiple de 30°, comme ce sera le cas pour tous les transformateurs complexes qui apparaîtront dans la suite de ce document, on l’exprime généralement sous forme d’indice horaire : par exemple, si \(\arg(\mu) = \frac{\pi}{6}\) (soit 30°), on dit que l’indice horaire est égal à 1h.

2.2 Passage d’impédance d’un côté à l’autre d’un transformateur idéal

2.2.1 Passage d’une impédance série

Considérons un transformateur idéal de rapport complexe \(\mu\) avec une impédance série \(Z\) au primaire. On peut modéliser ce circuit par les équations

\begin{equation}
\begin{cases}
V – Z I = \mu v \\
I + \frac{i}{\mu^*} = 0
\end{cases}
\end{equation}

soit

\begin{equation}
\begin{cases}
\frac{1}{\mu} V = v – \frac{Z}{|\mu|^2} i \\
I + \frac{i}{\mu^*} = 0,
\end{cases}
\end{equation}

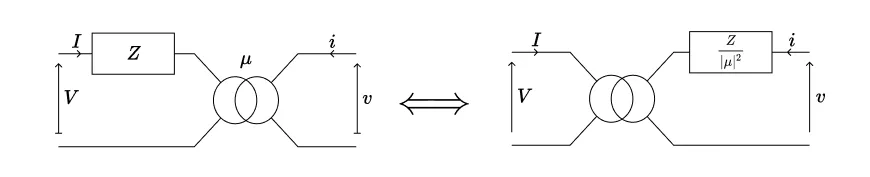
que l’on identifie au modèle d’un circuit composé du même transformateur idéal avec, cette fois, une impédance de valeur

\[ z := \frac{Z}{|\mu|^2} \]

placée en série du côté du secondaire. La situation est représentée ci-dessous :

Passage d'une impédance série de part et d'autre d'un transformateur idéal

2.2.2 Passage d’une admittance transverse

Considérons un transformateur idéal de rapport complexe \(\mu\) avec une admittance transverse au primaire. On peut modéliser ce circuit par les équations

\begin{equation}
\begin{cases}
V = \mu v \\
i + \mu^* (I – Y V) = 0
\end{cases}
\end{equation}

soit

\begin{equation}
\begin{cases}
V = \mu v \\
I + \frac{1}{\mu^*} (i – |\mu|^2 Y v) = 0
\end{cases}
\end{equation}

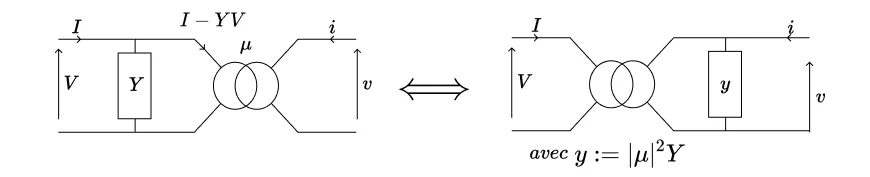
que l’on identifie au modèle d’un circuit composé du même transformateur idéal avec, cette fois, une admittance transverse de valeur

\[ y := |\mu|^2 Y \]

placée du côté du secondaire. La situation est représentée ci-dessous.

Passage d'une impédance transverse de part et d'autre d'un transformateur idéal

2.3 Circuit auxiliaire utile à l’étude des transformateurs non-idéaux

2.3.1 Mise en équations

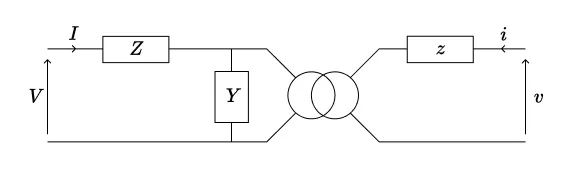
Circuit auxiliaire à deux impédances série, qui nous sera utile pour l'étude du transformateur monophasé non-idéal

Considérons le circuit de la figure ci-dessus, composé d’un transformateur idéal à rapport de transformation complexe \(\mu\), de deux admittances en série et d’une admittance transverse. Cette dernière a été placée arbitrairement du côté primaire ; comme nous l’avons vu dans la partie 2.2, elle pourrait aussi bien être placée du côté secondaire.

L’admittance transverse \(Y\) est traversée par le courant \(I + \frac{i}{\mu^*}\), et on peut donc modéliser notre circuit par les équations

\begin{equation}
\label{eq:circuit-auxiliaire-transfo-complexe}
\begin{cases}
V = (Z + \frac{1}{Y}) I + \frac{i}{\mu^* Y}\\
v = (z + \frac{1}{|\mu|^2 Y}) i + \frac{I}{\mu Y}.
\end{cases}
\end{equation}

Nous verrons fréquemment apparaître dans la suite de ce document des systèmes d’équations qui présentent cette structure, ce qui nous conduira à les identifier au circuit représenté ici.

Dans le cas où le transformateur est à rapport de transformation réel, ces équations précédentes deviennent

\begin{equation}
\label{eq:circuit-auxiliaire-transfo-reel}
\begin{cases}
V = (Z + \frac{1}{Y}) I + \frac{i}{\alpha Y}\\
v = (z + \frac{1}{\alpha^2 Y}) i + \frac{I}{\alpha Y}
\end{cases}
\end{equation}

où l’on a noté \(\alpha := \frac{N}{n}\) le rapport de transformation du transformateur.

2.3.2 Interprétation de la tension aux bornes de l’admittance transverse

Dans le cas où le rapport de transformation est réel, on observe que la tension aux bornes de l’admittance \(Y\) est égale à

\begin{equation}
\label{eq:UY-circuit-auxiliaire}
U_Y := \frac{1}{Y} (I + \frac{n}{N} \, i) = \frac{1}{NY} (NI + ni).
\end{equation}

Au facteur \(\frac{1}{NY}\) près, ceci montre que la tension \(U_Y\) nous donne la force magnétomotrice totale \(NI+ni\) qui s’exerce sur le circuit magnétique du transformateur. Connaissant la réluctance du circuit magnétique, ceci permet ensuite de calculer le flux dans le circuit magnétique ; d’où, connaissant la section du circuit magnétique, on pourra tirer l’intensité du champ magnétique. Enfin, la connaissance de l’intensité du champ magnétique nous permettra d’évaluer les pertes fer. Ce raisonnement reviendra plusieurs fois, sous différentes formes, dans la suite de cet ouvrage.

2.4 Modélisation du transformateur non-idéal à deux enroulements

Revenons à notre transformateur monophasé non-idéal à deux enroulements, représenté ci-dessous.

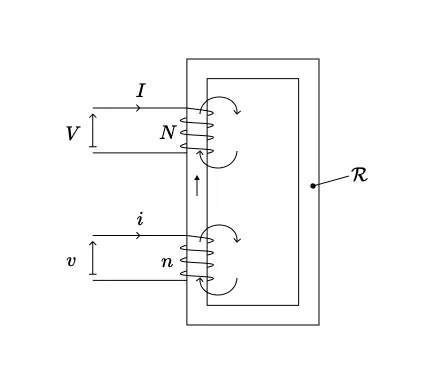
Transformateur monophasé
On modélise ce transformateur en tenant compte pour le moment des résistances \(R\) et \(r\) du bobinage primaire et du bobinage secondaire respectivement, et de leurs flux de fuite \(\Psi\) et \(\psi\) ; et de la réluctance \(\mathcal{R}\) du circuit magnétique. En revanche, on néglige pour le moment les pertes fer : celles-ci seront intégrées au modèle ultérieurement. Les équations associées sont les suivantes :
\begin{equation} \label{eq:transformateur-monophase-non-ideal-modele-electromagnetique} \begin{cases} V = R I + N j \omega (\phi + \Psi) \\ v = r i + n j \omega (\phi + \psi) \\ N I + n i = \mathcal{R} \, \phi \\ N I = \mathcal{R}^f \, \Psi \\ n i = \mathcal{R}^f \, \psi, \end{cases} \end{equation}
où l’on a considéré qu’aux flux de fuite s’opposait une certaine réluctance \(\mathcal{R}^f\) supposée identique au primaire et au secondaire. En éliminant les variables de flux magnétique et en introduisant les inverses \(\mathcal{Y}\) des réluctances \(\mathcal{R}\), ce système devient
\begin{equation} \begin{cases} V = \big(R + j \omega N^2 \mathcal{Y} + j \omega L^f\big) \, I + \frac{i}{\frac{N}{n} \frac{1}{j \omega N^2 \mathcal{Y}}} \\ v = \big(r + j \omega n^2 \mathcal{Y} + j \omega l^f) i + \frac{I}{\frac{N}{n} \frac{1}{j \omega N^2 \mathcal{Y}}}. \end{cases} \end{equation}
où l’on a introduit \[ L^f := N^2 \, \mathcal{Y}^f \quad \mbox{et} \quad l^f := n^2 \, \mathcal{Y}^f. \] Si l’on souhaite retrouver ultérieurement la variable de flux \(\phi\) que l’on a éliminée, on pourra utiliser
\begin{equation} \label{eq:phi-transfo-mono} \phi = \mathcal{Y} (NI + ni). \end{equation}
Par comparaison avec l’équation \(\eqref{eq:circuit-auxiliaire-transfo-reel} \), on observe que notre modèle de transformateur non-idéal est équivalent au circuit précédent avec \[ Y := \frac{1}{j \omega N^2 \, \mathcal{Y}}, \] \[ Z = R + j \omega N^2 \mathcal{Y} + j \omega L^f – \frac{1}{Y} = R + j \omega L^f \] et \[ z = r + j \omega n^2 \mathcal{Y} + j \omega l^f – \frac{1}{\alpha^2 \, Y} = r + j \omega l^f. \] On observe également que la tension \(U_Y\) aux bornes de l’admittance \(Y\), que nous avons calculée en (\ref{eq:UY-circuit-auxiliaire}), vérifie
\begin{equation} \label{eq:UY-transfo-mono} U_Y = \frac{1}{NY} (NI + ni) = (j \omega N \, \mathcal{Y}) \, (NI+ni)) = j \omega N \phi \end{equation}
où la dernière égalité vient de (\ref{eq:phi-transfo-mono}). Cette équation montre que la tension aux bornes de l’admittance \(Y\) de notre circuit auxiliaire est égale, au facteur \(j \omega N\) près, au flux dans le circuit magnétique ; nous allons exploiter cette propriété dans la section suivante consacrée à la modélisation des pertes fer.

2.4.1 Intégration des pertes fer

On considère généralement que les pertes fer volumiques, dans un matériau magnétique donné soumis à un champ magnétique sinusoïdal à fréquence donnée, sont approximativement proportionnelles au carré du module \(B\) du phaseur de champ magnétique. Autrement dit, on considère qu’elles sont de la forme \(\alpha |B|^2\), où \(\alpha\) (en \(A^2 \cdot s \cdot kg^{-1} \cdot m^{-1}\)) est un paramètre dont la valeur est déterminée par la nature du matériau magnétique et par la fréquence à laquelle il est utilisé. Au vu de (\ref{eq:UY-transfo-mono}), l’intensité du champ magnétique \(B\) dans notre modèle de transformateur monophasé est donnée par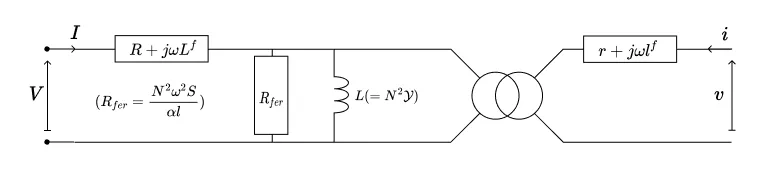
\begin{equation} B = \frac{\phi}{S} = \frac{U_Y}{j \omega N S}. \end{equation}
Les pertes fer totales sur l’ensemble du volume \(Sl\) du circuit magnétique sont donc égales à \[ (S l) \alpha \frac{|U_Y|^2}{(N S \omega)^2} = \frac{ \alpha l}{N^2 \omega^2 S} |U_Y|^2. \] Ces pertes sont identiques à celles que produirait une résistance de valeur
\begin{equation} R_f := \frac{N^2 \omega^2 S}{\alpha l} \end{equation}
soumise à la tension \(U_Y\) : c’est ce qui justifie l’introduction d’une telle résistance \(R_f\) en parallèle avec l’admittance \(Y\) dans le modèle de notre transformateur monophasé. Avec cette modification du modèle, le circuit électrique qui modélise le transformateur non-idéal est celui qui est représenté sur la Figure~ ci-dessous. Dans ce modèle, la valeur des inductances de fuite \(L^f\) et \(l^f\) ne peut guère être estimée qu’en effectuant des essais sur le transformateur réel, tandis que les autres paramètres peuvent être, au choix : soit calculés à partir des caractéristiques physiques des bobinages (pour \(R\) et \(r\)) et du circuit magnétique (pour \(R_f\) et \(L\)), soit estimés en procédant à des essais sur le transformateur réel.
Modèle de transformateur monophasé à deux impédances série, avec pertes fer

2.4.2 Modèle à une seule impédance série

Dans certaines situations, on peut considérer que le courant transverse est faible devant le courant série, autrement dit que les courants série au primaire et au secondaire sont égaux au facteur \(\mu\) près :

\begin{equation}
\label{eq:approx-transfo-mono}
i \approx – \mu^* I.
\end{equation}

Cette approximation est d’autant meilleure que le transformateur est « de bonne qualité » (forte inductance magnétisante, faibles pertes fer) et qu’il est chargé (forts courants série).

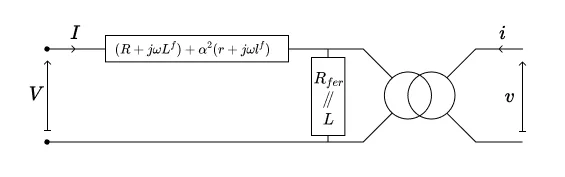
Cette approximation permet de passer l’impédance \(Z\) à droite de l’admittance \(Y\) dans le circuit de la figure initiale}, puis de la passer à droite du transformateur idéal (partie 2.2), et enfin de l’agréger avec l’impédance \(z\). La situation est représentée sur la figure ci-dessous :

Modèle de transformateur monophasé à une seule impédance série, au secondaire

Remarque : L’approximation (\ref{eq:approx-transfo-mono}) est très répandue, et le modèle de la figure ci-dessus qu’elle permet d’obtenir est « le » modèle usuel par excellence de transformateur monophasé non-idéal. Cette approximation est pourtant assez contestable : le courant magnétisant qui traverse l’admittance transverse n’est généralement pas si faible que ça, tandis que le courant série peut très bien être faible, si le transformateur est peu chargé.Considérons notamment le cas le plus extrême dans lequel l’approximation (\ref{eq:approx-transfo-mono}) ne s’applique manifestement pas : celui où l’on alimente le transformateur par le côté secondaire et où le primaire est laissé à vide : dans ce cas, le fait de ramener au primaire l’impédance série du secondaire revient à faire complètement disparaître celle-ci du modèle. Inversement, si l’on alimente le primaire et que le secondaire est laissé à vide, les non-idéalités du bobinage secondaire (résistance \(r\) et inductance de fuite \(l^f\)) interviennent dans le calcul, alors que le bobinage en question n’est traversé par aucun courant… Ces situations illustrent les limites du modèle à une seule impédance série, et invitent à lui préférer le modèle à deux impédances série, d’autant plus que celui-ci n’est guère plus compliqué.

Inversement, dans le cadre d’une étude de court-circuit, le courant série sera généralement très élevé : non seulement l’approximation (\ref{eq:approx-transfo-mono}) est alors beaucoup plus justifiée, mais on va même souvent jusqu’à négliger complètement l’admittance transverse.

Remarque : Le modèle de la Figure ci-dessous singularise le côté primaire par rapport au secondaire : si l’on avait décidé de ramener les impédances série vers le côté primaire, et non pas vers le côté primaire, on aurait obtenu un modèle différent, celui présenté ci-dessous.
Modèle de transformateur monophasé non-idéal à une seule impédance série, celle-ci étant placée (de façon inhabituelle) du côté primaire, en amont de l'admittance transverse

2.5 Modélisation du transformateur à trois enroulements

En suivant le même type de raisonnement que pour le transformateur monophasé à deux enroulements, on propose pour le transformateur monophasé à trois enroulement le modèle à une seule impédance série (par enroulement secondaire) qui est représenté sur la Figure ci-dessous.

Modèle de transformateur monophasé à trois enroulements

Nos autres articles